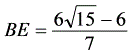如图,在梯形ABCD中,AD//BC,AB=CD=BC=6,AD=3.点M为边BC的中点,以M为顶点作∠EMF=∠B,射线ME交腰AB于点E,射线MF交腰CD于点F,连结E
F、(1)求证:△MEF∽△BEM;(2)若△BEM是以BM为腰的等腰三角形,求EF的长;(3)若EF⊥CD,求BE的长.
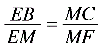………………………………………………………1分∵MC=MB,∴
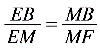,又∠EMF=∠B,∴△MEF∽△BEM ……………………1分(2)若BM=BE=3=MC,由△EBM∽△EMF∽△MFC,∴CF=MF=3,EF=
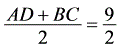2分若BM=EM=3=MC,由△EBM∽△EMF∽△MFC,∴F与D重合,DE=CD=6,即EF=6…2分(3)EF⊥CD,△MEF∽△BEM,∴∠MFE=∠MFC=∠BME=45° …………………………2分解一:过点E作 EH⊥BC ………………………………………………………………………………1分设BE=x,则BH=
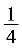x,EH=MH=
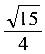x…………………………………………………………1分∴
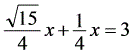,∴BE=x=
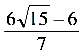…………………………………………………………2分解二:过点M作 MN⊥DC,MC=3, ,NC=
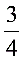. MN=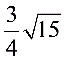
=FN,FC=
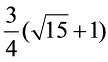--2由△MEF∽△MFC有
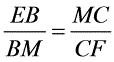即
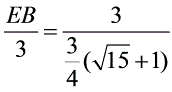,得BE=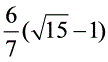
.--------------------------2解法3:如图3,分别延长BA、CD,交于点G设BE=x,则FC=
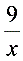易求得:AG=DG=6∴EG=12-x,FG=
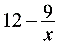又在等腰△GBC中,可求得cos∠G=
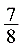∴在Rt△GEF中,cos∠G=
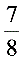,EG=12-x,FG=
∴
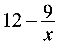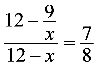解得: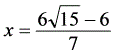
∴
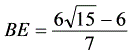解法四:如图4,分别延长AD、CB,分别交直线EF于点Q、点P易求得:cosC= cos∠FDQ=
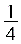,设BE=x,则FC=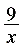
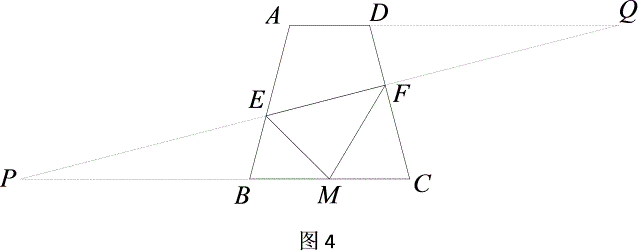∴PC=4FC=
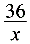,DQ=4DF=
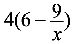,∴PB=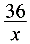
-6,AQ=
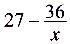,∵AQ//PB∴
∴
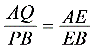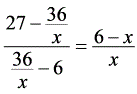解得: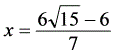
∴
