习题解答例题1(习题7.3):
习题解答例题1(习题7.3):
发布时间:2026-01-25 19:42:09
习题解答例题1(习题7.3):
 费米能级的定义式(7.44)求得
费米能级的定义式(7.44)求得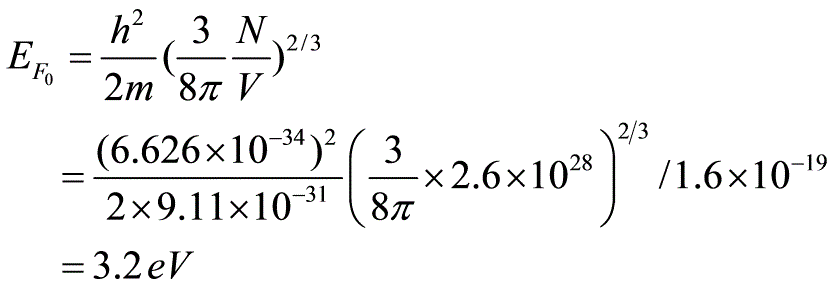 温度为室温时, Na的费米能级的近似值由式(7.55)有
温度为室温时, Na的费米能级的近似值由式(7.55)有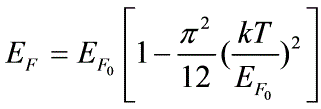
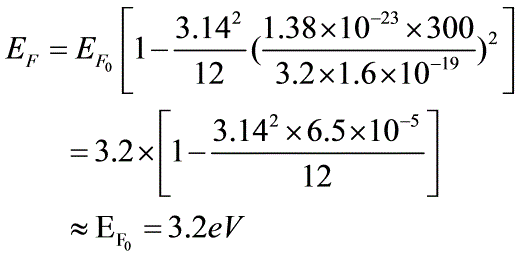 (2) 取1mol的电子,此时电子比热近似值由(7.57)式有
(2) 取1mol的电子,此时电子比热近似值由(7.57)式有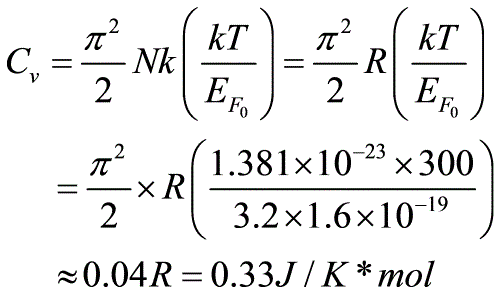 例题2(习题7.4和7.5):解:(1) 单位时间内碰到单位面积的器壁上的电子数,由式(6.87)为(在这儿:为电子的平均速率)
例题2(习题7.4和7.5):解:(1) 单位时间内碰到单位面积的器壁上的电子数,由式(6.87)为(在这儿:为电子的平均速率)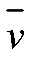 (此式适用于一切理想气体)由式(6.20)并考虑到电子的简并度,则在体积V内,动量绝对值在
(此式适用于一切理想气体)由式(6.20)并考虑到电子的简并度,则在体积V内,动量绝对值在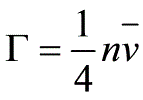 到范围内电子的状态数为
到范围内电子的状态数为 又考虑到绝对零度下电子气体中电子动量的分布为其中
又考虑到绝对零度下电子气体中电子动量的分布为其中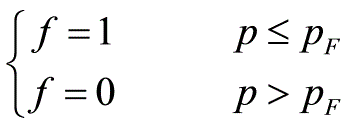 为费米动量,也即绝对零度时电子的动量,这样电子的平均动量为
为费米动量,也即绝对零度时电子的动量,这样电子的平均动量为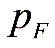 所以电子的平均速率为(习题7.5)由式(7.45),费米动量有所以(2) 由内能的热力学微分方程有由上式可得,在温度不变时,则有由式(7.46)有
所以电子的平均速率为(习题7.5)由式(7.45),费米动量有所以(2) 由内能的热力学微分方程有由上式可得,在温度不变时,则有由式(7.46)有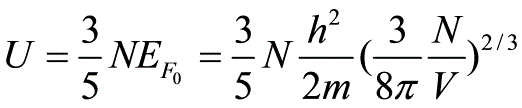 例题3(习题7.6)解:由式(6.20)并考虑到电子的简并度,在体积V内,动量绝对值在到范围内,自由粒子的可能的状态数为(参考上题)考虑到在相对论下,有
例题3(习题7.6)解:由式(6.20)并考虑到电子的简并度,在体积V内,动量绝对值在到范围内,自由粒子的可能的状态数为(参考上题)考虑到在相对论下,有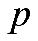 ,这样结合上式可得在体积V内,在
,这样结合上式可得在体积V内,在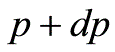 到能量范围内量子态数为
到能量范围内量子态数为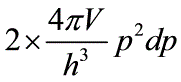 又考虑到绝对零度下电子气体的分布为
又考虑到绝对零度下电子气体的分布为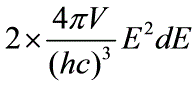 费米能级由下式决定
费米能级由下式决定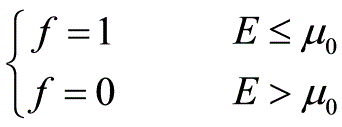 即可得到在绝对零度下相对论理想气体的费米能级为
即可得到在绝对零度下相对论理想气体的费米能级为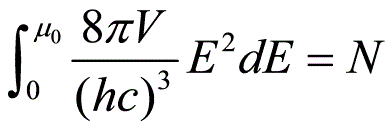 在绝对零度下相对论理想气体的内能也即总能量为
在绝对零度下相对论理想气体的内能也即总能量为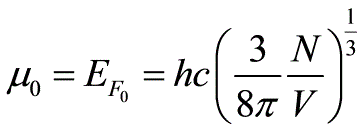 例题4(习题7.13)解:(1)如果粒子可分辨,令其分别为a和b则有(2)如果粒子不可分辨,但不受Pauling原理限制,
例题4(习题7.13)解:(1)如果粒子可分辨,令其分别为a和b则有(2)如果粒子不可分辨,但不受Pauling原理限制,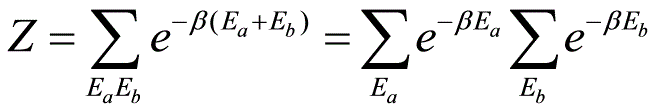 (对于Bose分布,粒子数占据能级的可能性有六种(0,0),(0,1),(0,2),(1,1),(1,2),(2,2) )(3)粒子不可分辨且服从Pauling原理(对于Fermi分布,粒子数占据能级的可能性有三种(0,1),(0,2), (1,2))例题5(习题7.14)解:在单位体积中其动量在间隔的状态数为其中,所以
(对于Bose分布,粒子数占据能级的可能性有六种(0,0),(0,1),(0,2),(1,1),(1,2),(2,2) )(3)粒子不可分辨且服从Pauling原理(对于Fermi分布,粒子数占据能级的可能性有三种(0,1),(0,2), (1,2))例题5(习题7.14)解:在单位体积中其动量在间隔的状态数为其中,所以 当时
当时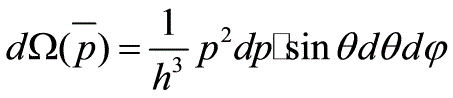
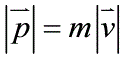 其中,
其中,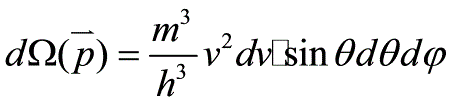 ,所以
,所以
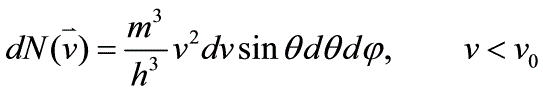
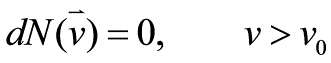 注:
注: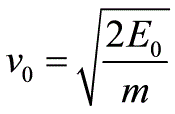
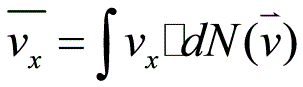 例题6(习题7.15)解:(1)首先判别该电子气服从哪种统计由第132页式(6.73)可知
例题6(习题7.15)解:(1)首先判别该电子气服从哪种统计由第132页式(6.73)可知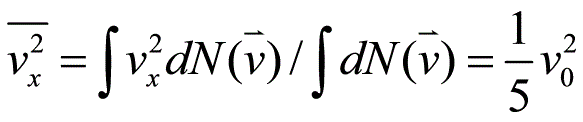 则由第150页式(7.12)和(7.14)可得,当非简并性条件满足时,Bose分布和Fermi分布过渡到Boltzmann分布。所以在本题中的电子气体服从Boltzmann统计分布,这时自由电子的能量与动量的关系为由能量均分定理可知(2)此电子气可视为经典的理想气体,所以其物态方程为
则由第150页式(7.12)和(7.14)可得,当非简并性条件满足时,Bose分布和Fermi分布过渡到Boltzmann分布。所以在本题中的电子气体服从Boltzmann统计分布,这时自由电子的能量与动量的关系为由能量均分定理可知(2)此电子气可视为经典的理想气体,所以其物态方程为
