今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.(1)求温馨提示牌和垃圾箱的单价各是多少元?(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
∴
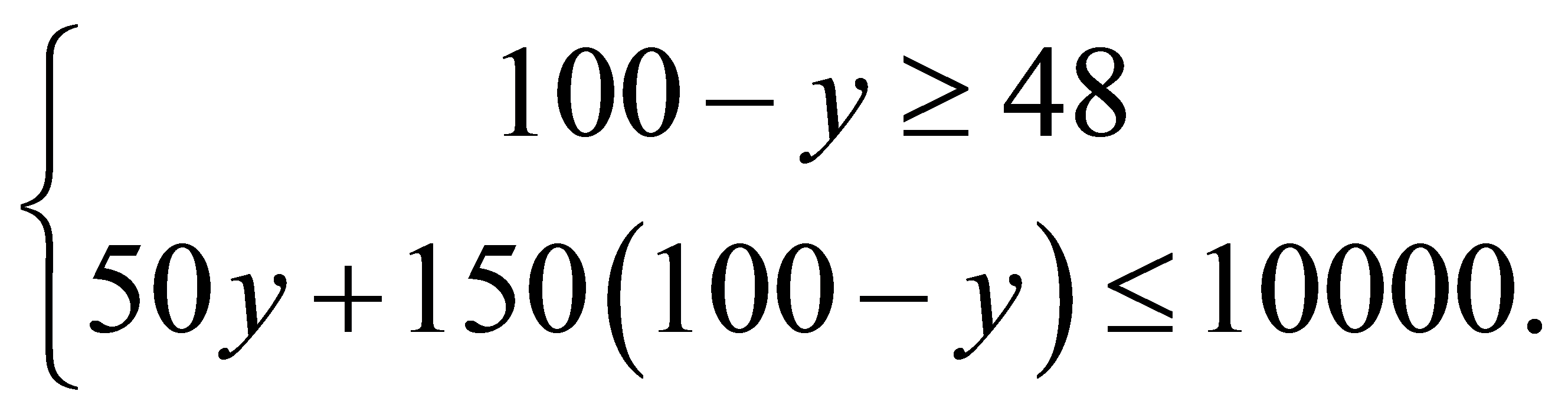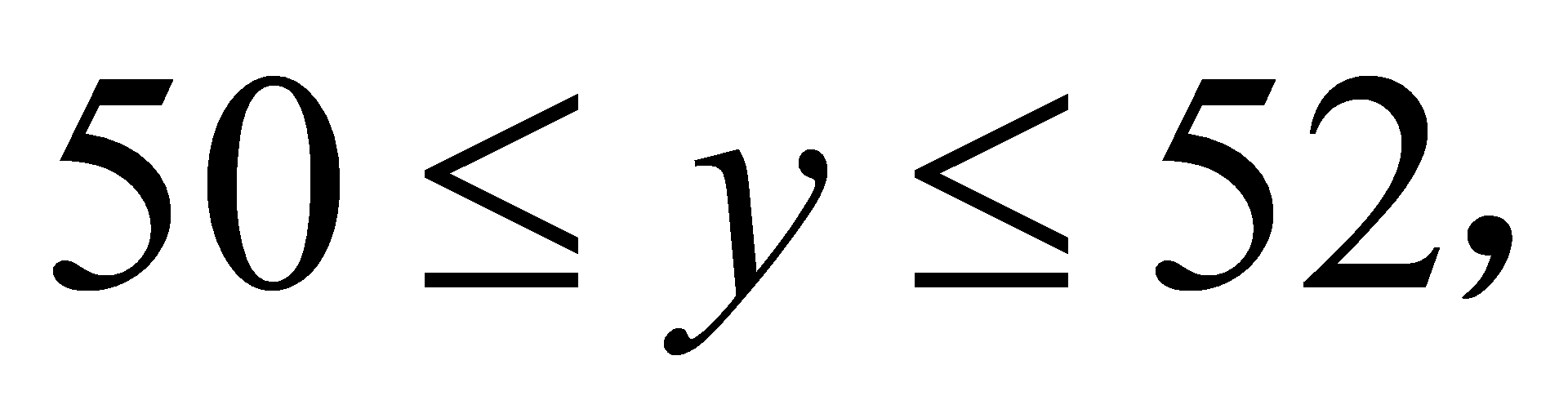∵y为正整数,∴y为50,51,52,共3中方案;有三种方案:①温馨提示牌50个,垃圾箱50个,②温馨提示牌51个,垃圾箱49个,③温馨提示牌52个,垃圾箱48个,设总费用为w元W=50y 150(100﹣y)=﹣100y 15000,∵k=-100
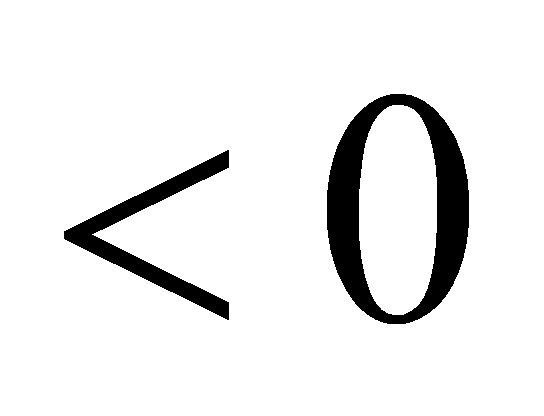,∴w随y的增大而减小∴当y=52时,所需资金最少,最少是9800元.[点睛]此题主要考查了一元一次不等式组,一元一次方程的应用,正确找出相等关系是解本题的关键.9.2019年暑假期间,某学校计划租用8辆客车送280名师生参加社会实践活动,现有甲、乙两种客车,它们的载客量和租金如表,设租用甲种客车x辆,租车总费用为w元.甲种客车乙种客车载客量（人/辆）3040租金（元/辆）270320(1)求出w(元)与x(辆)之间函数关系式,并直接写出自变量x的取值范围;(2)选择怎样的租车方案所需的费用最低?最低费用多少元?[答案](1)(且x为整数);(2)租用甲种客车4辆,租用乙种客车4辆,所需的费用最低,为2360元.[解析](1)根据题意租金×客车数量=租车总费用列出方程即可,根据车辆不能超过计划数量8且要满足载客总数大于等于280人列出不等式求解即可;(2)根据(1)中得出的表达式判断w随x的增大而减小,再根据自变量x的取值范围取最大值求解即可.[详解]解:(1)设租用甲种客车x辆,则租用乙种客车辆,由题意可得出
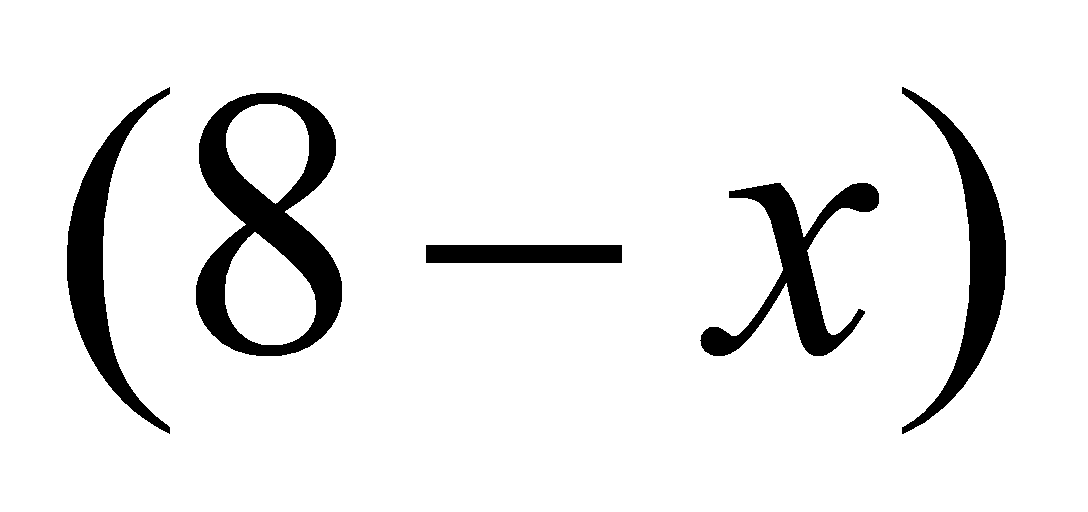由题意可知:
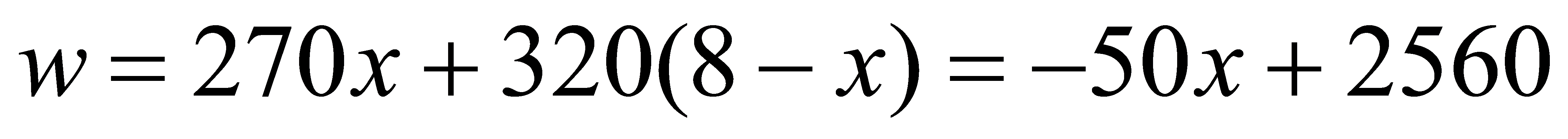解得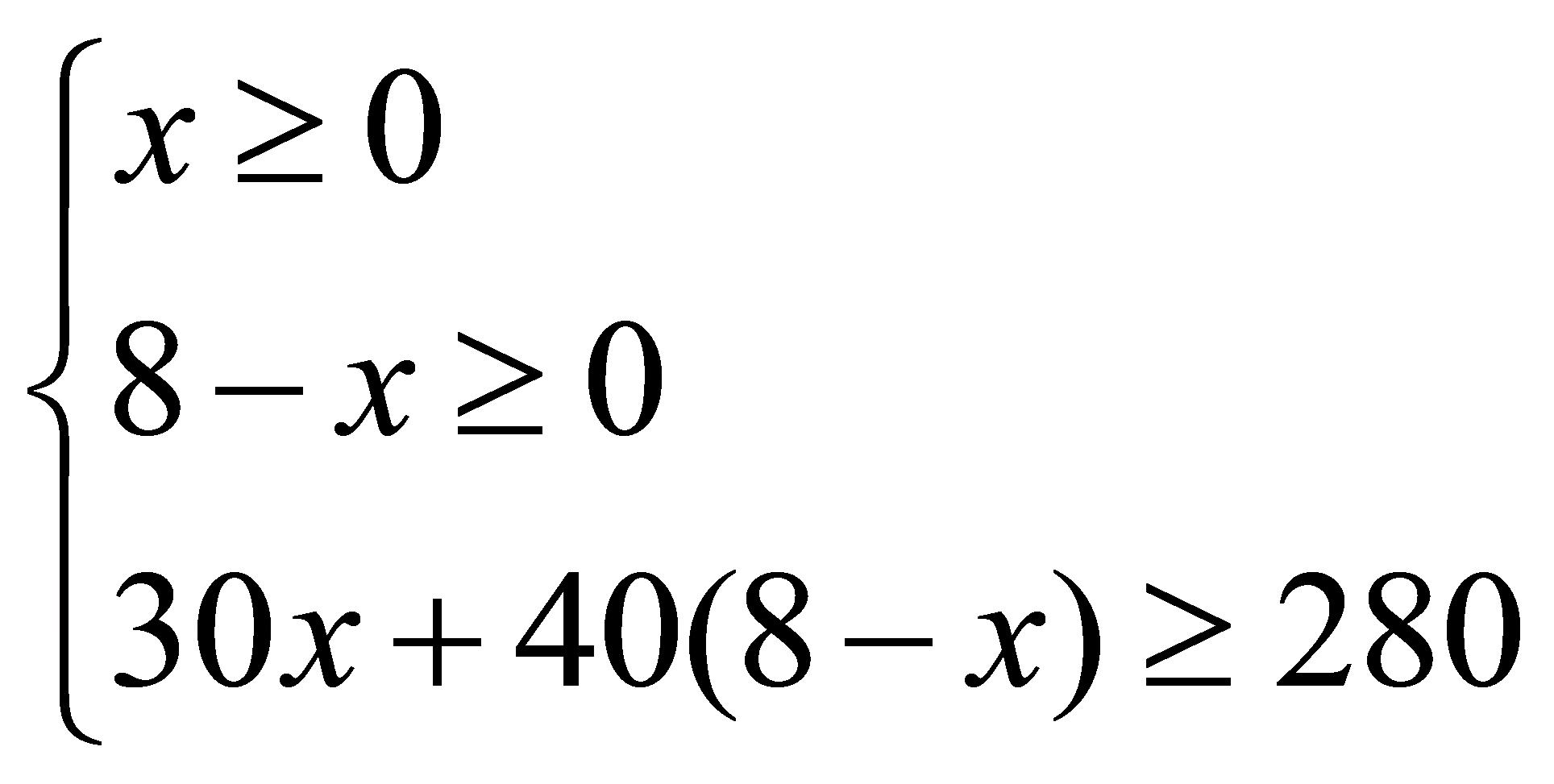
且x为整数∴自变量x的取值范围为:
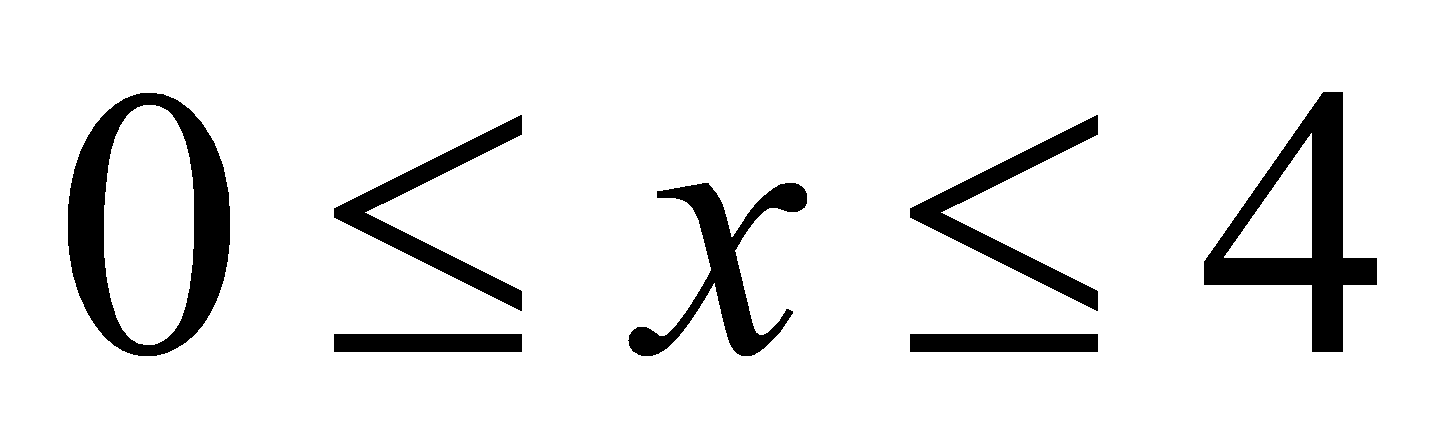且x为整数;(2)∵
中x的系数,∴w随x的增大而减小,∴当x取最大值时即时,w的值最小,其最小值为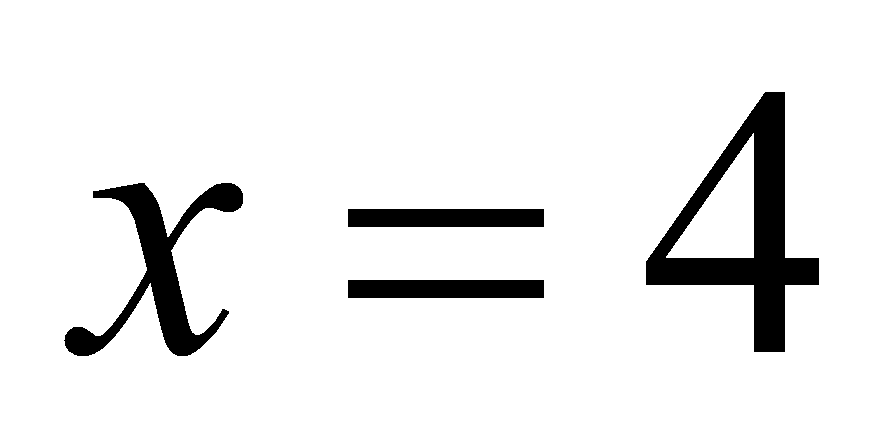
元,∴租用甲种客车4辆,租用乙种客车4辆,所需的费用最低,为2360元.[点睛]本题主要考查一次函数和一元一次不等式的应用,充分理解题意找出等量关系是关键.
