W(f(1)
W(f(1)
发布时间：2025-02-25 09:35:54
请在 下方输入 要搜索的题目：
推荐参考答案 (
由 快搜搜题库 官方老师解答 )
答案：
相关试题
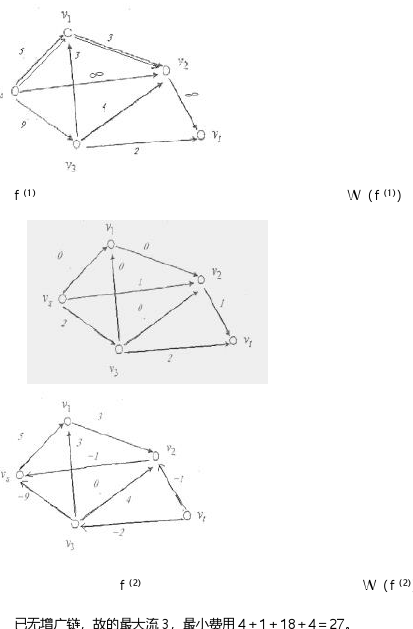
- 1.W(f(1)
- 2.8.已知f(t)→F(ji),且 ||>tm时,f(1)=0,试证明:F(j)=∑F(unsa2(-n).其中,w=,la≤2
- 3.|W 1 |>|W 2 |B.|W 1 | 2 |C.|W 1 |=|W 2 |D.无法比较
-
4.设f(x)=x2 bx c,且f(-1)=f(3),则( )A、f(1)>c>f(-1)B、f(1)
- 5.【单选题】int w = 0; void fun() { w++; printf("w = %d ", w); } main() { int w = 5; w++; printf("w = %d ",
- 6.F/W eng. (finished with engine)
- 7.В прямоугольнике W B D M WBDM провели F D ∣ ∣ W R FD∣∣WR так, что ∠ B D F = 30 ° ∠BDF=30°.
- 8.< /(j),^(x) < 1, / f(x)dx= [ ff(T)dx.Jo Jo求证: （Jq i/w 一 ”工)1血 < g
- 9.[(F/A M/W2)2 (T/W)2]3≤[0D.[(F/A M/W2)2 4(T/W)2]
- 10.对于函数f（n）=A、f（n 1）-f（n）=1B、f（n k）=f（n）（k∈N * ）C、α f（n） =f（n 1） αf（n）（α≠0）D、α f（n 1） =α-（α 1）f（n）（α≠0）
