在平面直角坐标系xOy中,圆C的方程为(x-1)2 y2=4,P为圆C上一点.若存在一个定圆M,过P作圆M的两条切线PA,PB,切点分别为A,B,当P在圆C上运动时,使得∠APB恒为60,则圆M的方程为 .
在平面直角坐标系xOy中,圆C的方程为(x-1)2 y2=4,P为圆C上一点.若存在一个定圆M,过P作圆M的两条切线PA,PB,切点分别为A,B,当P在圆C上运动时,使得∠APB恒为60,则圆M的方程为 .
发布时间:2025-04-04 10:35:28
在平面直角坐标系xOy中,圆C的方程为(x-1)2 y2=4,P为圆C上一点.若存在一个定圆M,过P作圆M的两条切线PA,PB,切点分别为A,B,当P在圆C上运动时,使得∠APB恒为60,则圆M的方程为 .
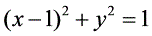 .[解析]∵当P在圆C上运动时∠APB恒为60°,∴圆M与圆C一定是同心圆,∴可设圆M的方程为(x-1)2 y2=r2.当点P坐标是(3,0)时,设直线AB与x轴的交点为H,则MH HP=2,MH=
.[解析]∵当P在圆C上运动时∠APB恒为60°,∴圆M与圆C一定是同心圆,∴可设圆M的方程为(x-1)2 y2=r2.当点P坐标是(3,0)时,设直线AB与x轴的交点为H,则MH HP=2,MH= ,AB=2×
,AB=2×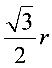 ,所以
,所以 2×
2× ×
× =2,解得r=1,所以所求圆M的方程为(x-1)2 y2=1;
=2,解得r=1,所以所求圆M的方程为(x-1)2 y2=1;
