- 首页
- 监理工程师
-
1.已知X~t(n),求证X2~F(1, n).
-
2.已知f(x)=T n ,证明:对?n∈N 有1≤T n <4.
-
3.设随机变量X ~ t(n),Y = 1/X2则( ).
-
4.已知函数f(x)=lnx-kx 1.N ,n>1).
-
5.已知函数 f( x )=x2 – 1 ,则 f(1)= ( C )
-
6.已知T n . (3)证明:对?n∈N ,有1≤T n <4.
-
7.【答案】年 includefloat f (float x,int n)if(n==0)return 1;return (x*f (x, n-1));void main(float×;
-
8.已知f(1)=1,f(n)=f(n-1)+n,那么f(50)的作用是( )。
-
9.对于函数f(n)=A、f(n 1)-f(n)=1B、f(n k)=f(n)(k∈N * )C、α f(n) =f(n 1) αf(n)(α≠0)D、α f(n 1) =α-(α 1)f(n)(α≠0)
-
10.64.已知X1,x2,X3相互独立,且服从x~N(0,02),证明XI X X3服从t(1)分布
 , 其中
, 其中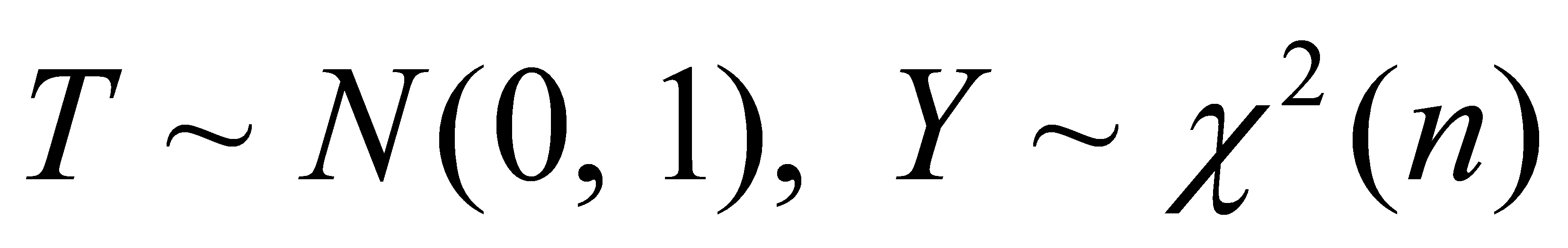 , 又因T与Y相互独立,故T2与Y相互独立,
, 又因T与Y相互独立,故T2与Y相互独立,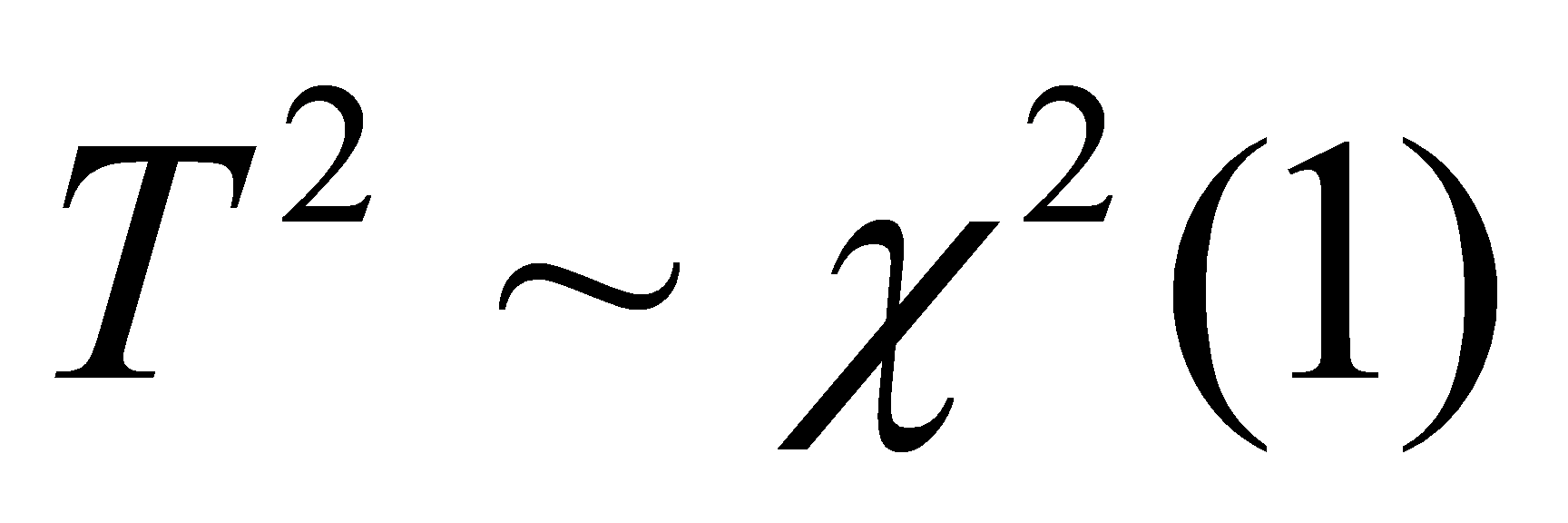 ,
,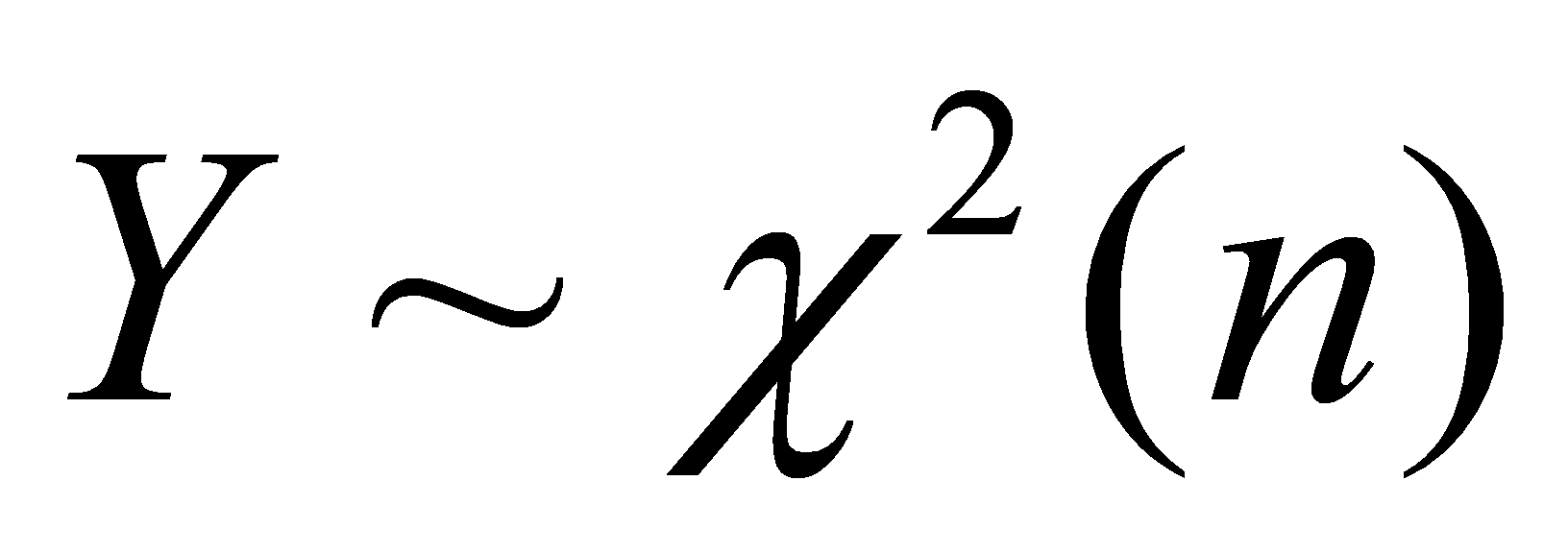 , 则
, 则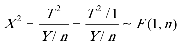 .
.
