考点:虚数,(集合),最大模原理 {难度:★★★★☆}{ 2016年第57届国际数学奥林匹克中国国家队选拔考试(CMO) }
考点:虚数,(集合),最大模原理 {难度:★★★★☆}{ 2016年第57届国际数学奥林匹克中国国家队选拔考试(CMO) }
发布时间:2025-07-12 23:42:33
考点:虚数,(集合),最大模原理 {难度:★★★★☆}{ 2016年第57届国际数学奥林匹克中国国家队选拔考试(CMO) }
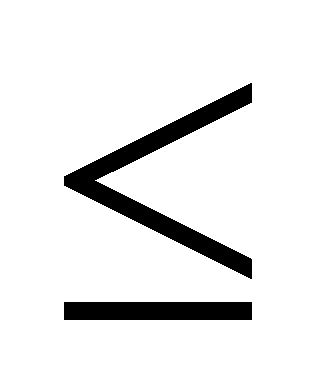 的情况。在高等数学中有最大模原理,解析函数在自变量在边界时达到最大模。所以,容易想到当
的情况。在高等数学中有最大模原理,解析函数在自变量在边界时达到最大模。所以,容易想到当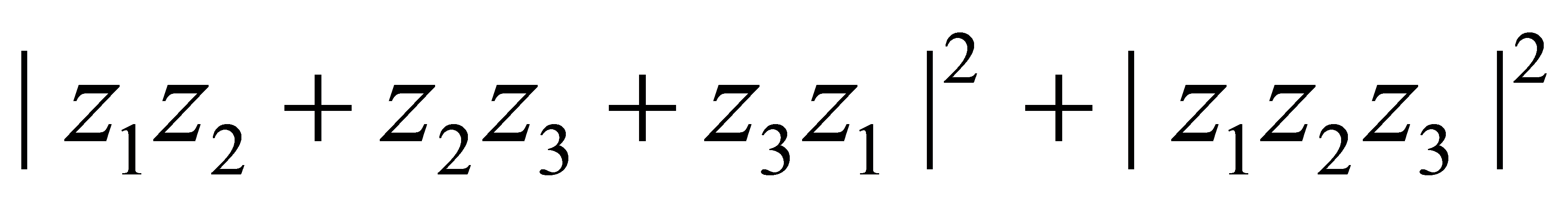 最大时,
最大时,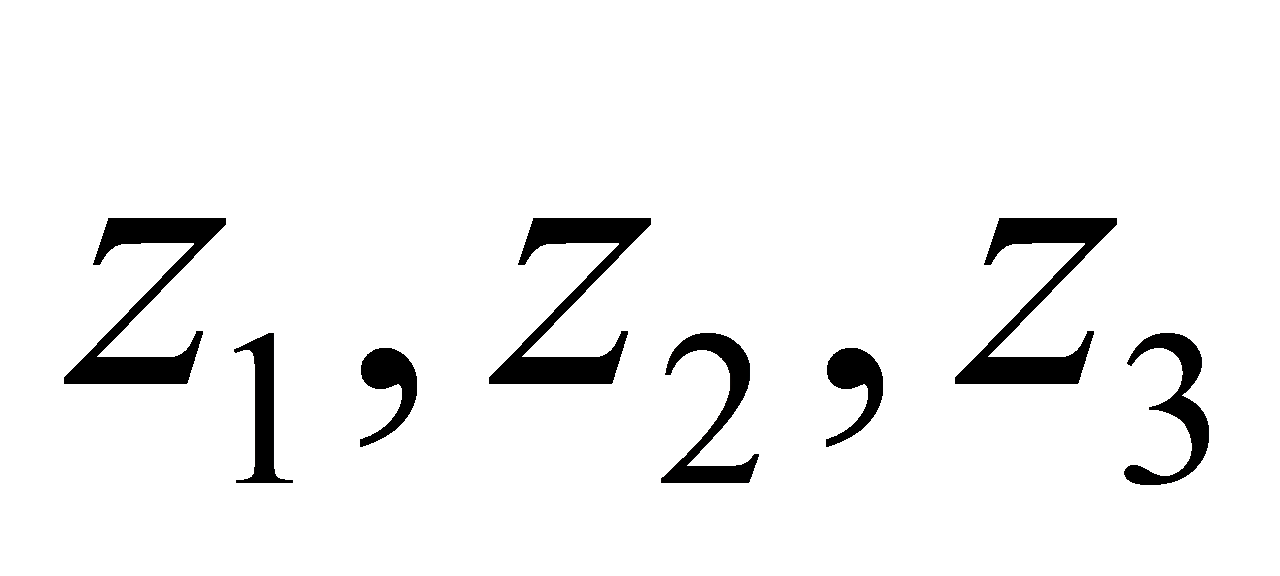 至少有两个在边界,即满足
至少有两个在边界,即满足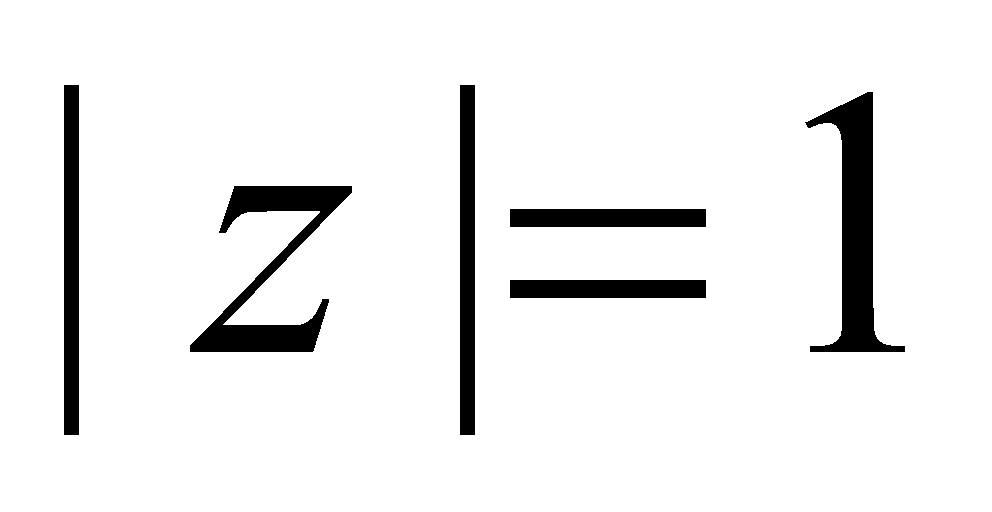 ,而
,而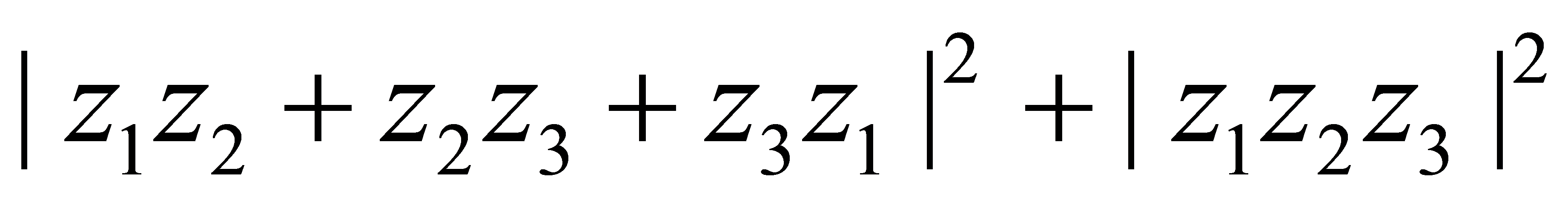 =
=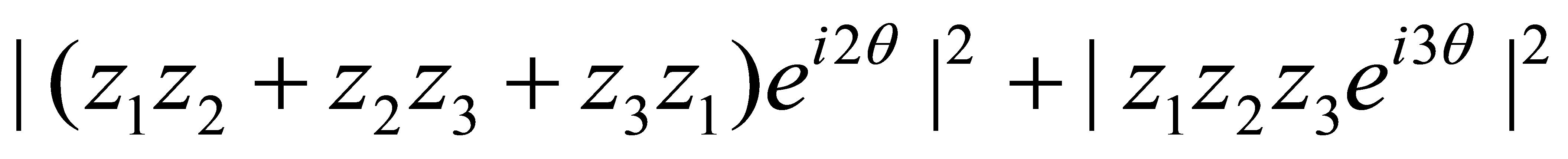 ,故不妨设
,故不妨设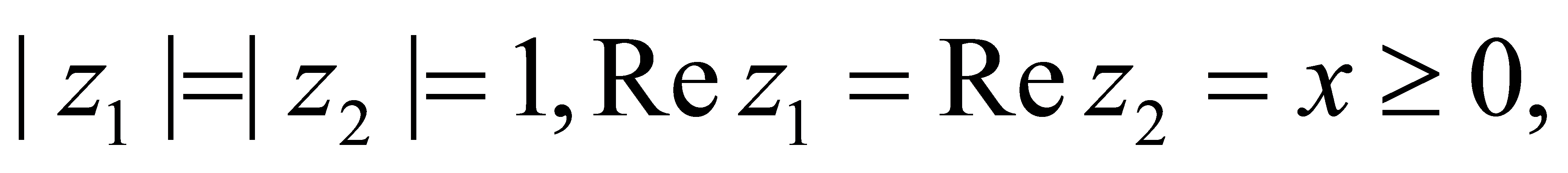 则
则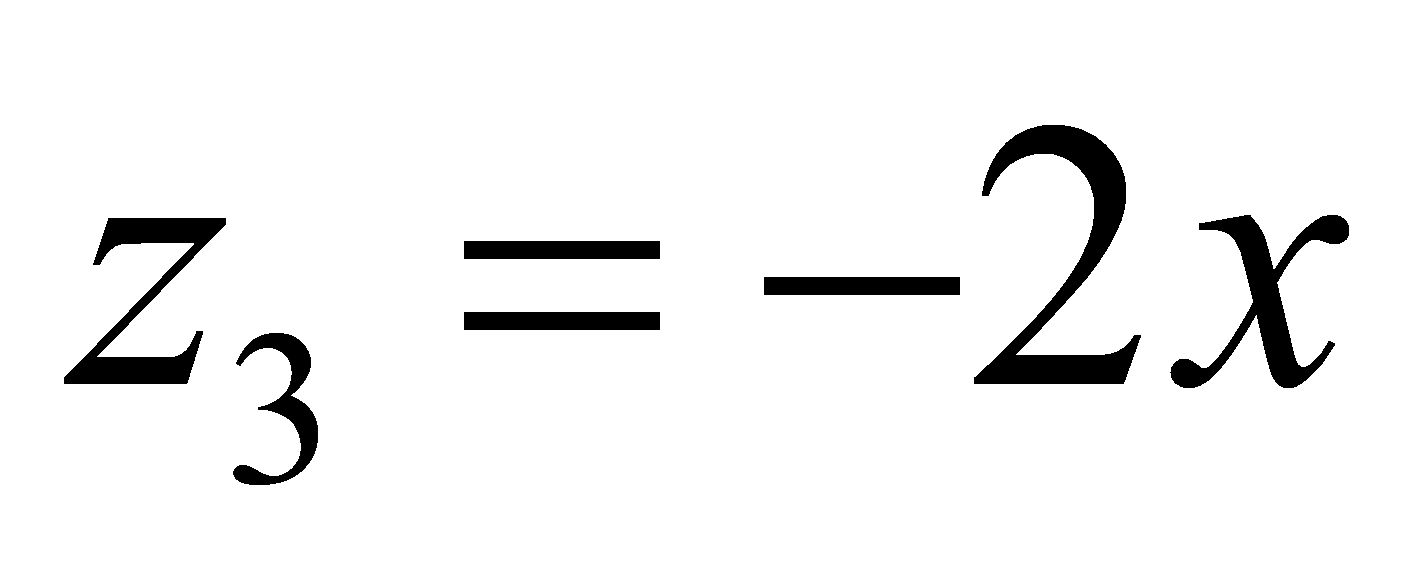 ,
,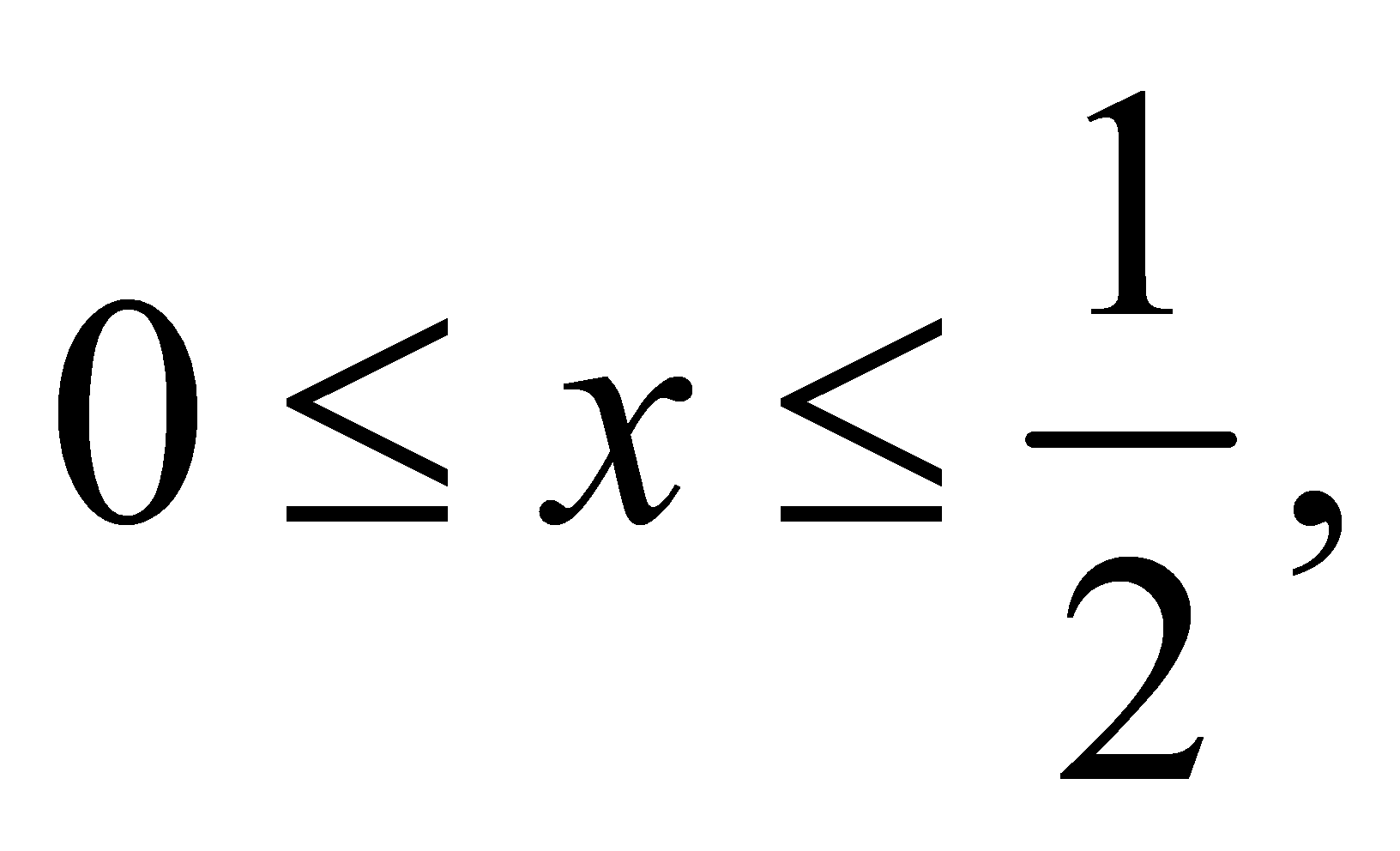 所以
所以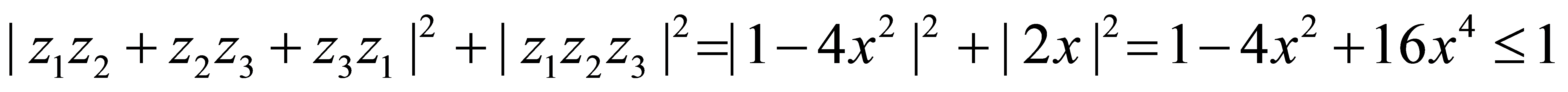 ,所以
,所以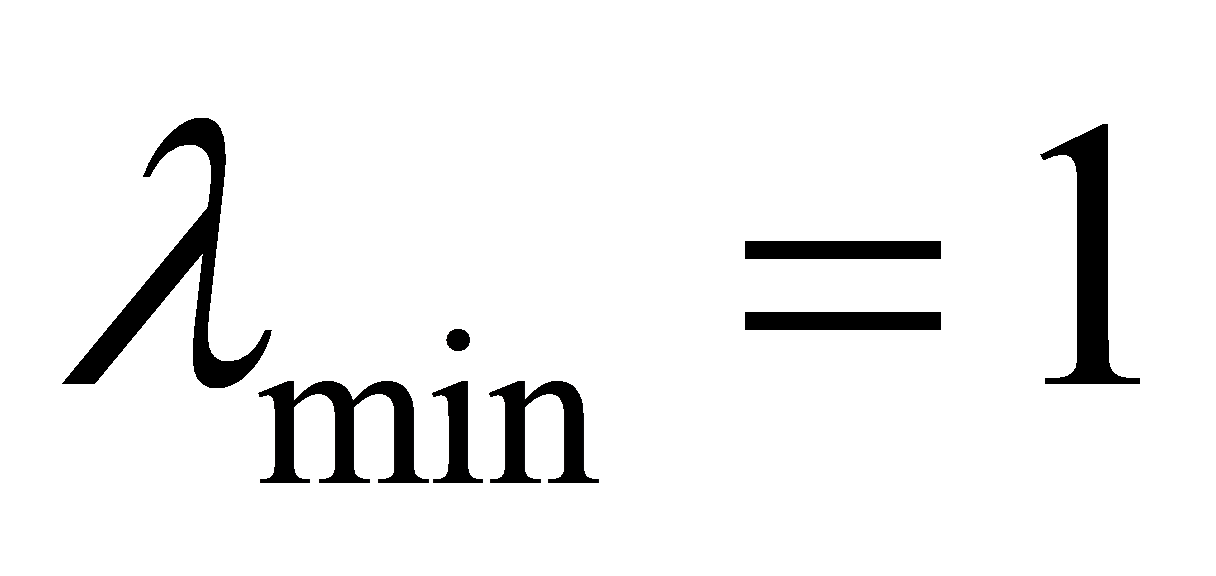 下面设法证明之。不妨设
下面设法证明之。不妨设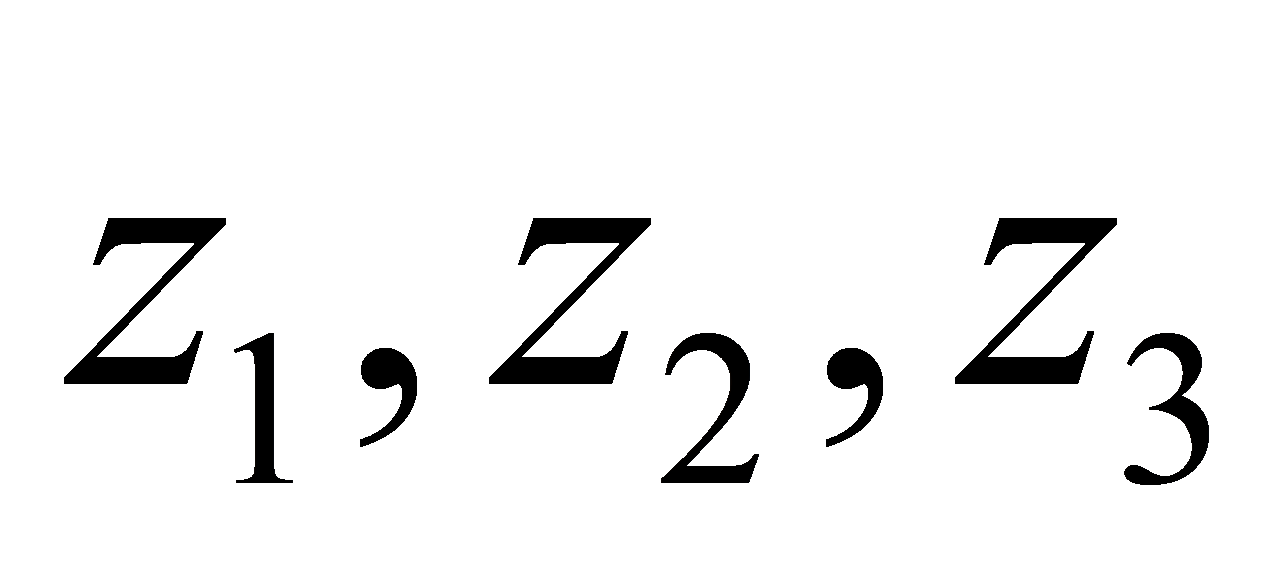 中
中 的模最大,因为
的模最大,因为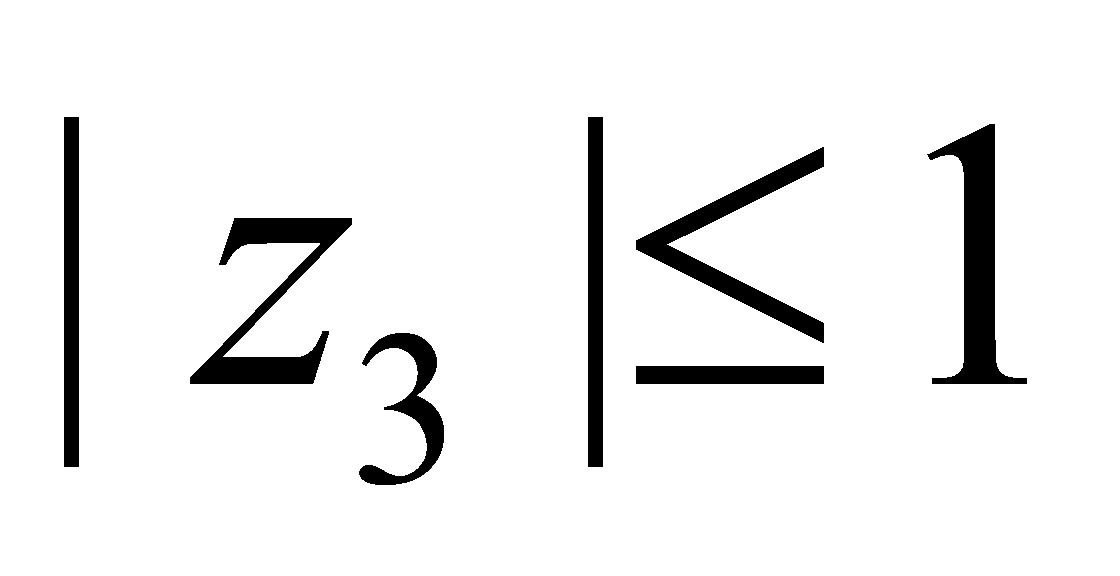 ,将每个数都乘以
,将每个数都乘以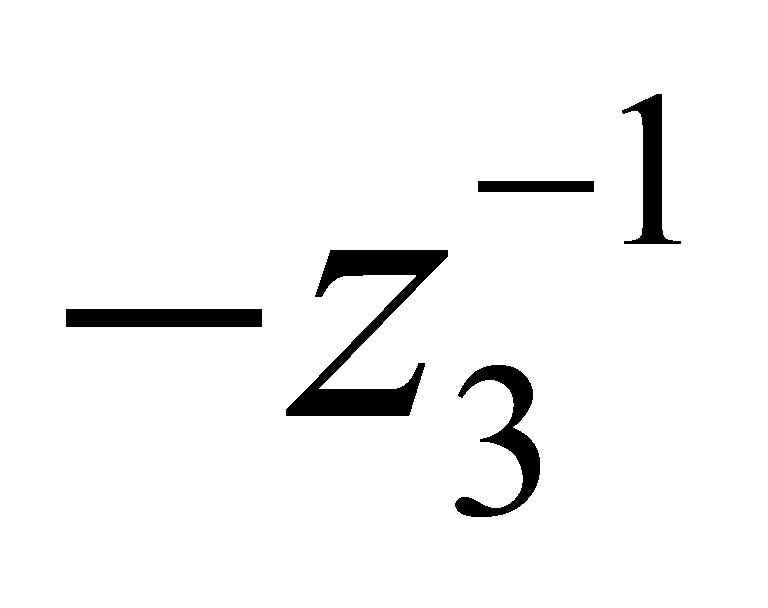 代替原来的数,则左边更大,此时
代替原来的数,则左边更大,此时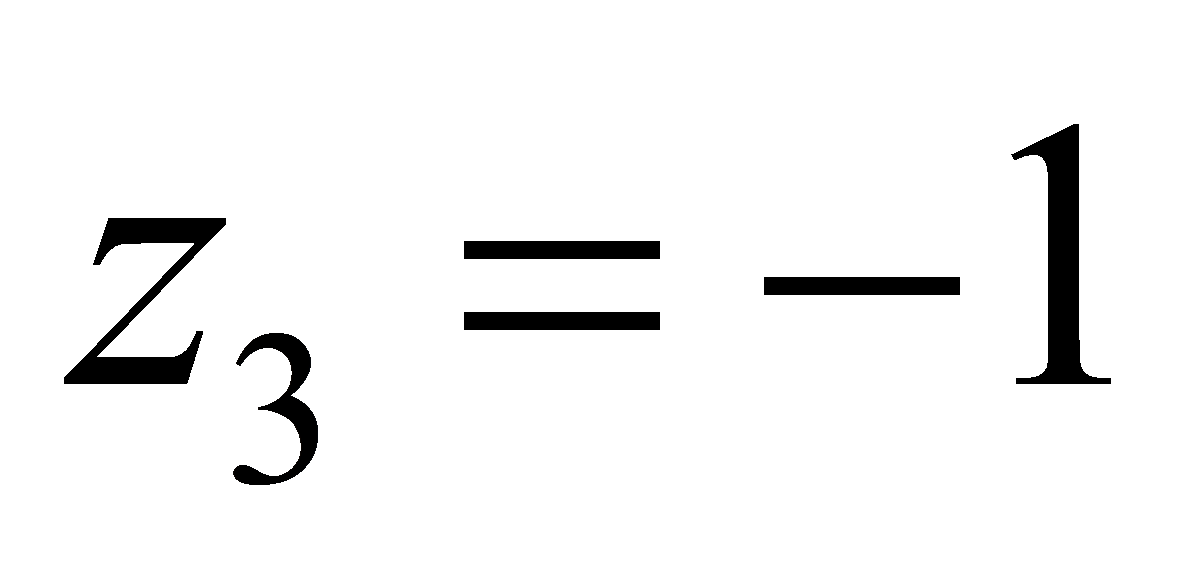 ,因为
,因为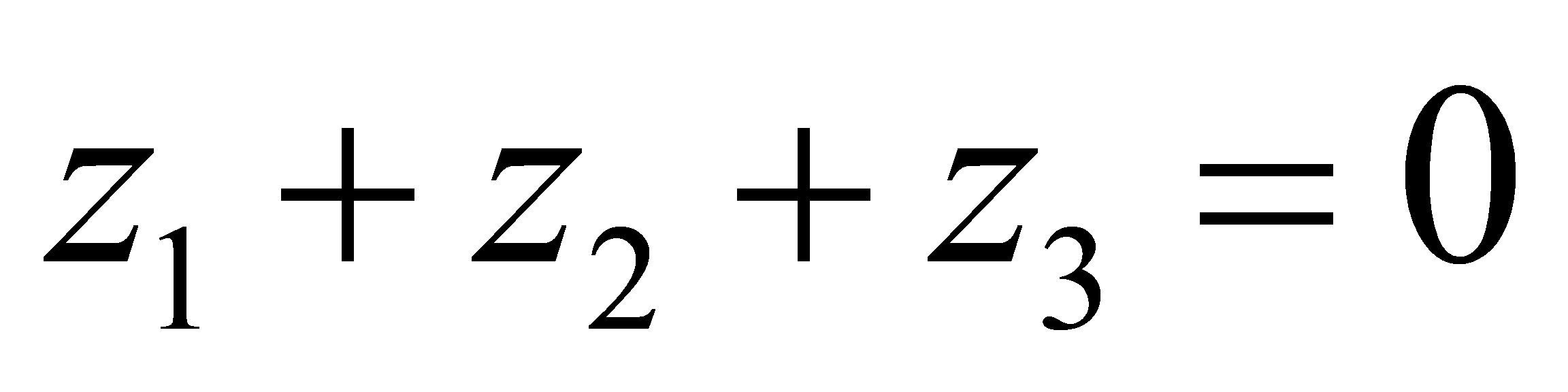 ,设
,设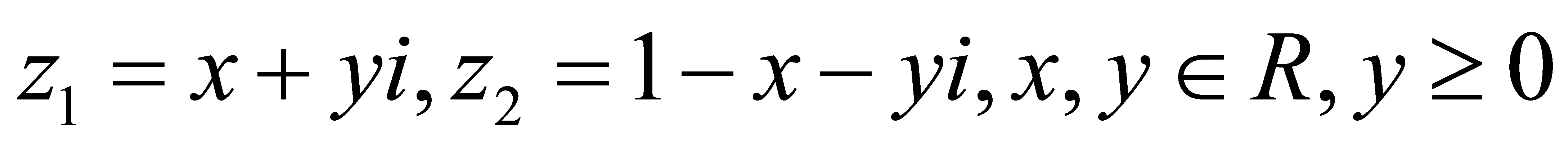 ,则
,则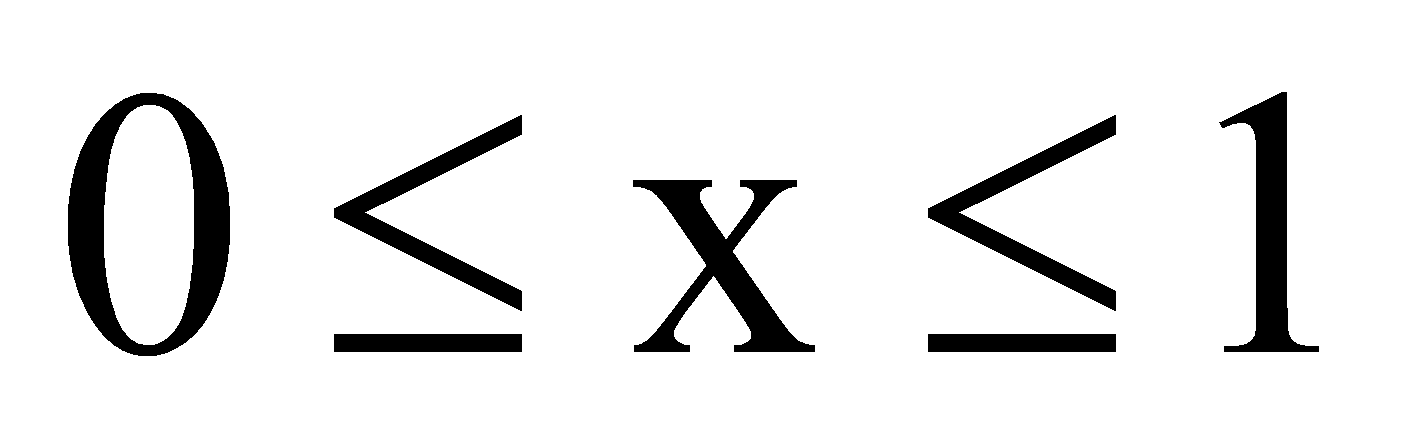 ,代入化简得
,代入化简得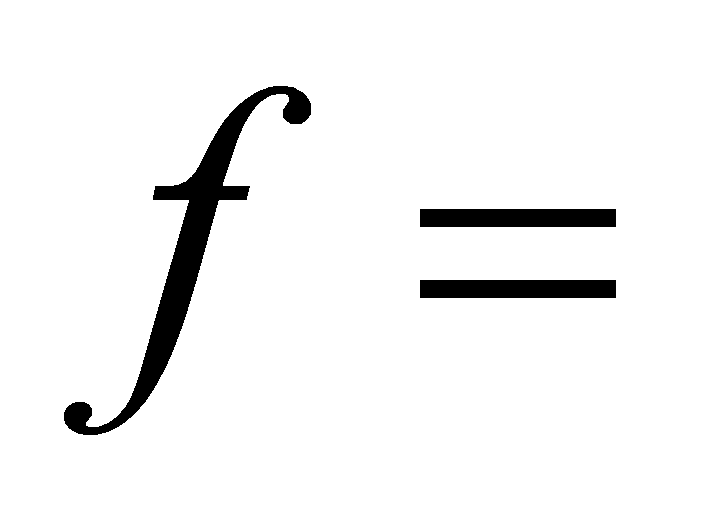 左边=
左边=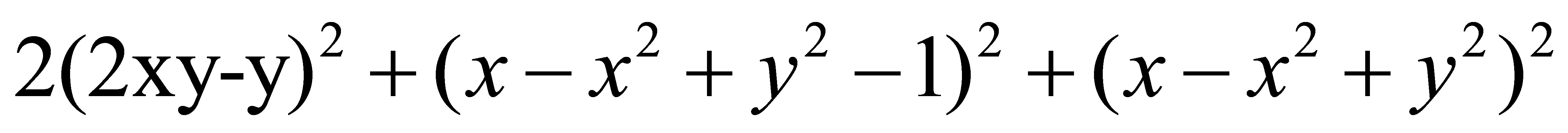 ,先固定x,得
,先固定x,得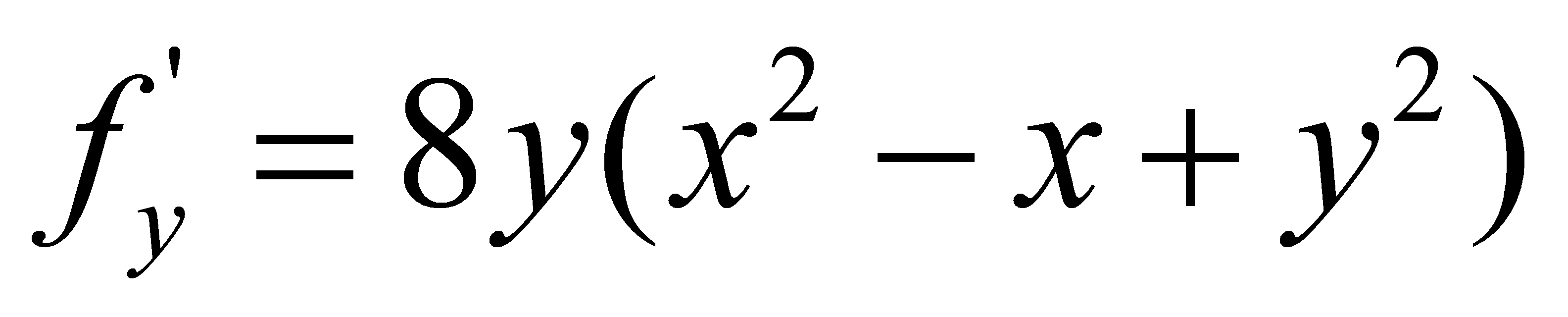 ,所以
,所以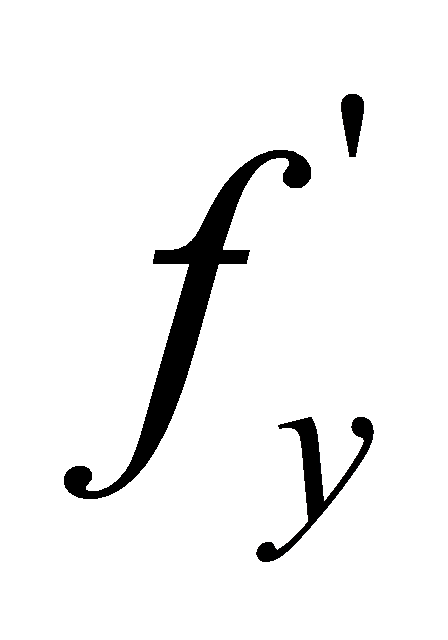 先负后正,
先负后正,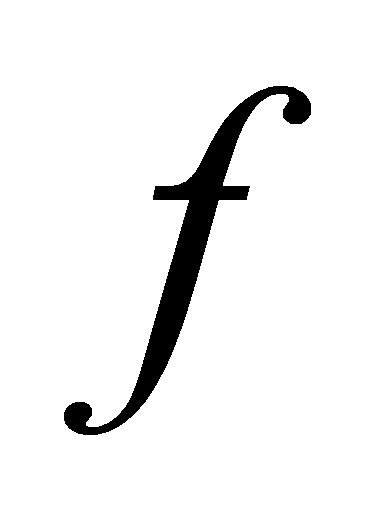 先减后增,在两端最大,当
先减后增,在两端最大,当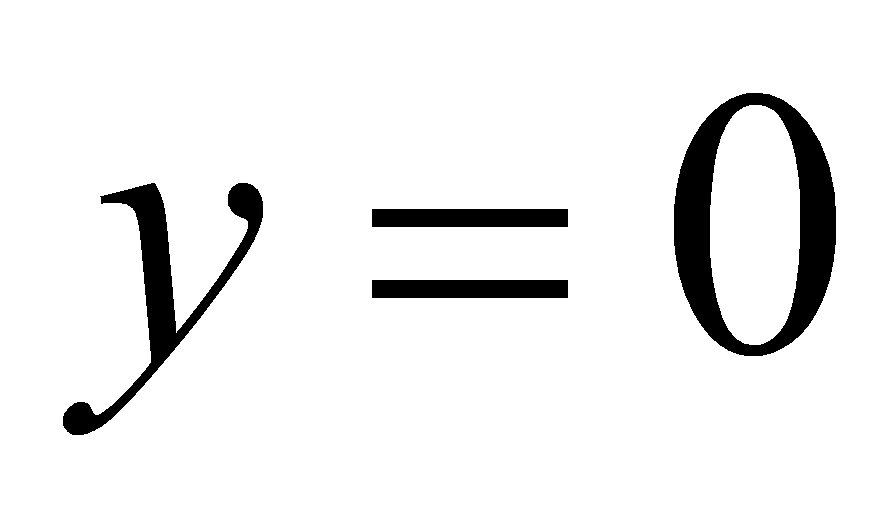 时,
时,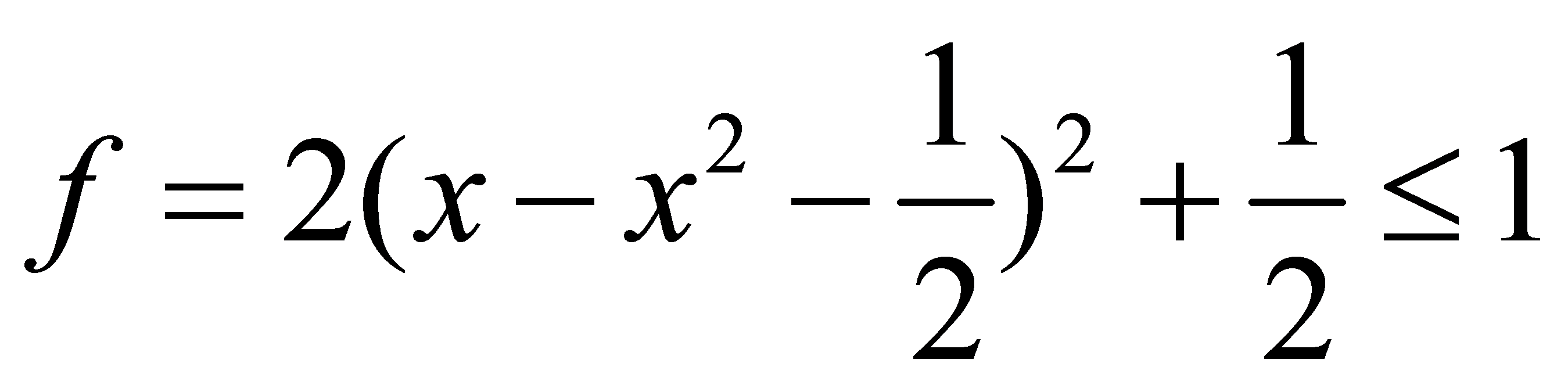 ,当
,当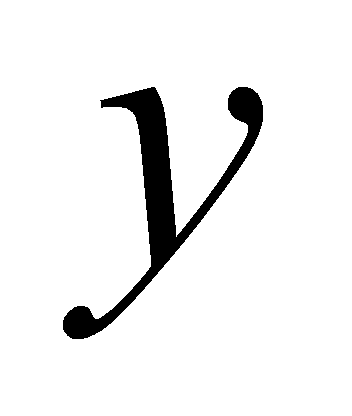 最大时,
最大时,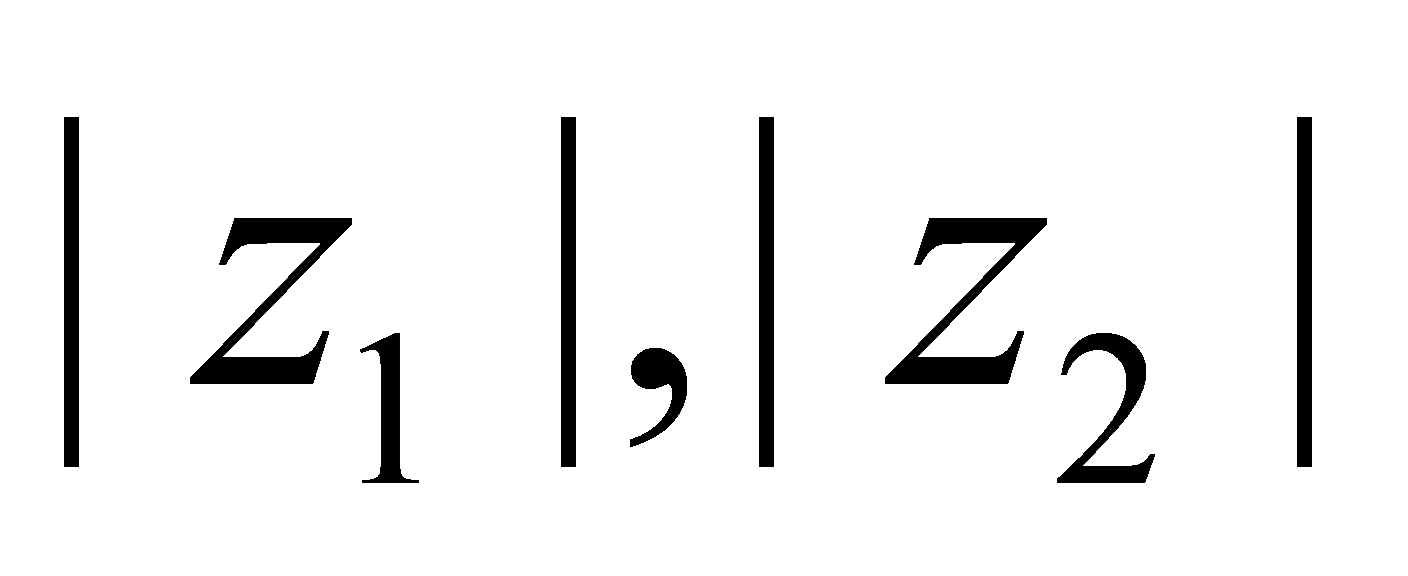 至少一个为1,不妨设
至少一个为1,不妨设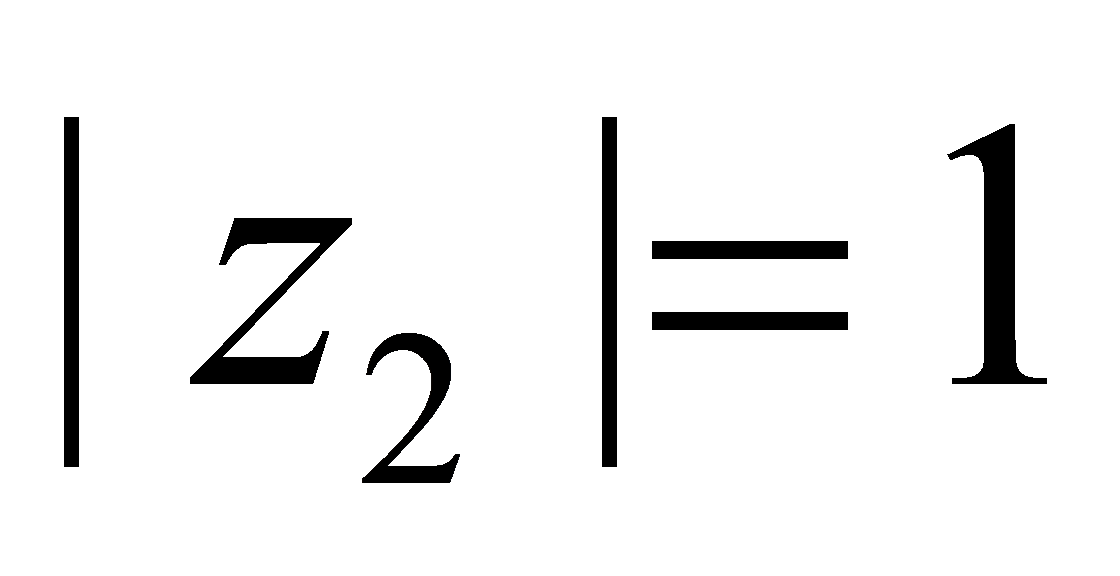 ,以下同前面分析,即旋转为
,以下同前面分析,即旋转为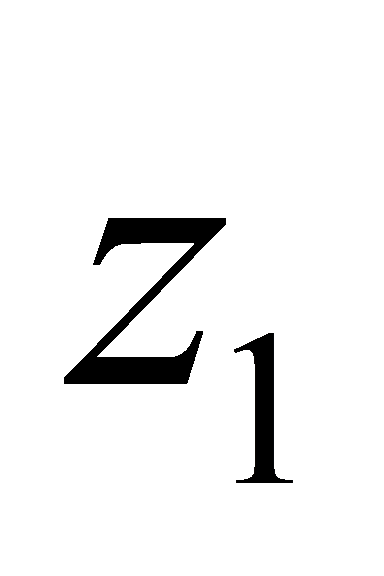 在x轴负半轴上,设
在x轴负半轴上,设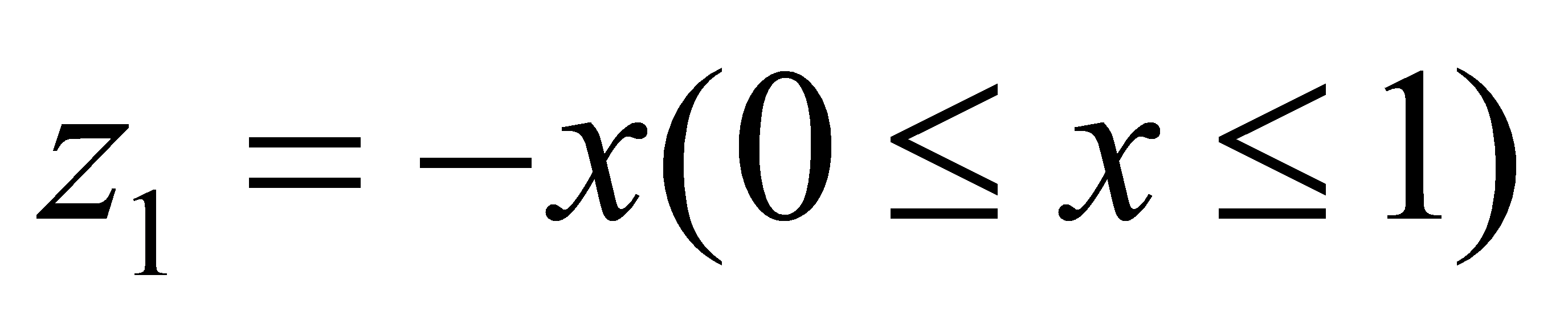 ,则左边
,则左边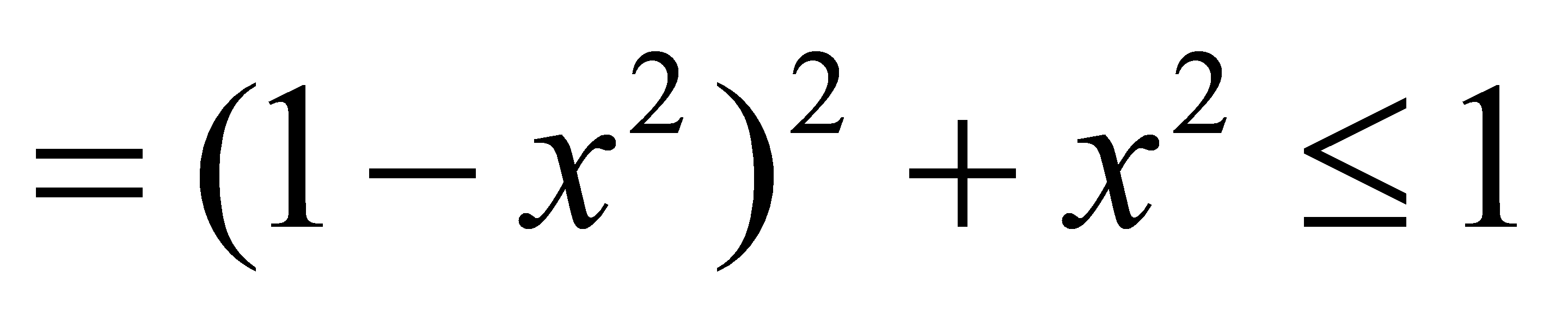 ,所以
,所以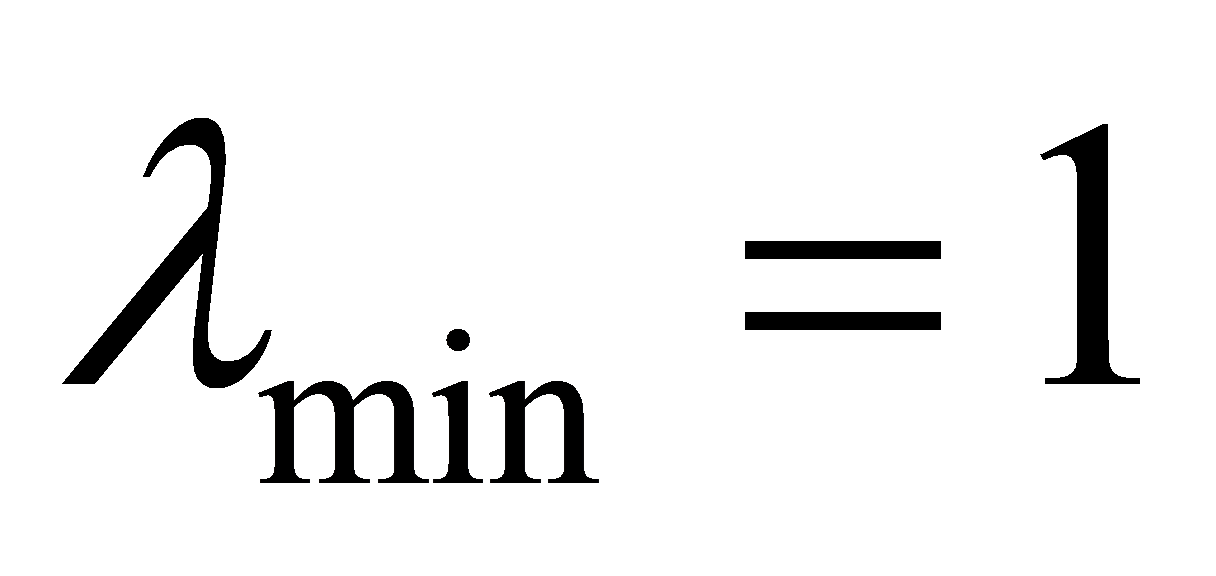 。
。
