https://bgk-photo.cdn.bcebos.com/doc/pic/item/0e2442a7d933c895784297bcd61373f08202003c.jpg如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2，与y轴交于点C（0，-4），其中x1，x2是方程x2-4x-12=0的两个根．（1）求抛物线的解析式；（2）点M是线段AB上的一个动点，过点M作MN∥BC，交AC于点N，连接CM，当△CMN的面积最大时，求点M的坐标；（3）点D（4，k）在（1）中抛物线上，点E为抛物线上一动点，在x轴上是否存在点F，使以A、D、E、F为顶点的四边形是平行四边形？如果存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．
https://bgk-photo.cdn.bcebos.com/doc/pic/item/0e2442a7d933c895784297bcd61373f08202003c.jpg如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2，与y轴交于点C（0，-4），其中x1，x2是方程x2-4x-12=0的两个根．（1）求抛物线的解析式；（2）点M是线段AB上的一个动点，过点M作MN∥BC，交AC于点N，连接CM，当△CMN的面积最大时，求点M的坐标；（3）点D（4，k）在（1）中抛物线上，点E为抛物线上一动点，在x轴上是否存在点F，使以
A、
D、
E、F为顶点的四边形是平行四边形？如果存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．
发布时间：2025-03-09 14:57:47
解：（1）∵x2-4x-12=0，∴x1=-2，x2=6．∴A（-2，0），B（6，0），又∵抛物线过点A、B、C，故设抛物线的解析式为y=a（x 2）（x-6），将点C的坐标代入，求得
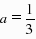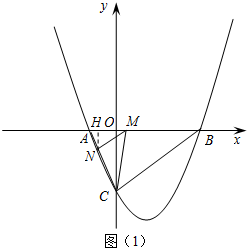
，∴抛物线的解析式为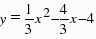
；（2）设点M的坐标为（m，0），过点N作NH⊥x轴于点H（如图（1））．∵点A的坐标为（-2，0），点B的坐标为（6，0），
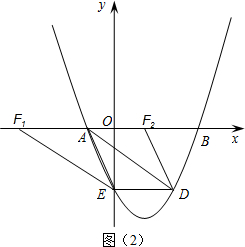∴AB=8，AM=m 2，∵MN∥BC，∴△MNA∽△BCA．∴
，∴
，∴
，∴
，=
，=
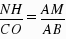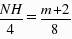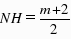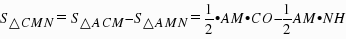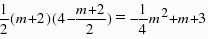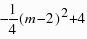．∴当m=2时，S△CMN有最大值4．此时，点M的坐标为（2，0）；（3）∵点D（4，k）在抛物线
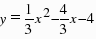上，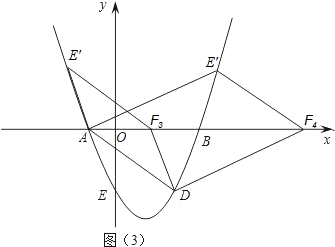
∴当x=4时，k=-4，∴点D的坐标是（4，-4）．①如图（2），当AF为平行四边形的边时，AF平行且等于DE，∵D（4，-4），∴DE=4．∴F1（-6，0），F2（2，0），②如图（3），当AF为平行四边形的对角线时，设F（n，0），∵点A的坐标为（-2，0），则平行四边形的对称中心的横坐标为：
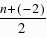，∴平行四边形的对称中心坐标为（
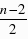，0），∵D（4，-4），∴E‘的横坐标为：
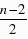-4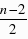 
=n-6，E'的纵坐标为：4，∴E'的坐标为（n-6，4）．把E'（n-6，4）代入
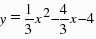，得n2-16n 36=0．解得
．
，
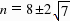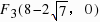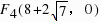，综上所述F1（-6，0），F2（2，0），F3（8-2
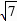，0），F4（8 2
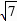，0）．
