如图,抛物线的图象与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,点D是抛物线的顶点,且A(﹣6,0),D(﹣2,﹣8).(1)求抛物线的解析式;(2)点P是直线AC下方的抛物线上一动点,不与点A、C重合,求过点P作x轴的垂线交于AC于点E,求线段PE的最大值及P点坐标;(3)在抛物线的对称轴上足否存在点M,使得△ACM为直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.https://bgk-photo.cdn.bcebos.com/0824ab18972bd4076ba4959c6b899e510fb3096b.jpg
如图,抛物线的图象与x轴交于
A、B两点,点A在点B的左边,与y轴交于点C,点D是抛物线的顶点,且A(﹣6,0),D(﹣2,﹣8).(1)求抛物线的解析式;(2)点P是直线AC下方的抛物线上一动点,不与点
A、C重合,求过点P作x轴的垂线交于AC于点E,求线段PE的最大值及P点坐标;(3)在抛物线的对称轴上足否存在点M,使得△ACM为直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.https://bgk-photo.cdn.bcebos.com/0824ab18972bd4076ba4959c6b899e510fb3096b.jpg
发布时间：2025-03-02 11:55:39
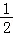x2 2x﹣6)(﹣6
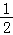,∴抛物线的解析式为y=
(x 2)2﹣8,即y=
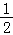x2 2x﹣6;(2)如图,当x=0时,y=
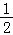x2 2x﹣6=﹣6,则C(0,﹣6),设直线AC的解析式为y=kx b,把A(﹣6,0),C(0,﹣6)代入得
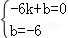,解得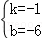
,∴直线AC的解析式为y=﹣x﹣6,设P(x,
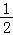x2 2x﹣6)(﹣6
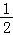x2﹣3x=﹣
(x 3)2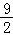 
,当x=﹣3时,PE的长度有最大值,最大值为
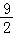,此时P点坐标为(﹣3,﹣
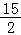);(3)存在.抛物线的对称轴为直线x=﹣2,设M(﹣2,t),∵A(﹣6,0),C(0,﹣6),∴AC2=62 62=72,AM2=(﹣2 6)2 t2,CM2=(﹣2)2 (t 6)2,当AC2 AM2=CM2,△ACM为直角三角形,即72 (﹣2 6)2 t2=(﹣2)2 (t 6)2,解得t=4,此时M点坐标为(﹣2,4);当AC2 CM2=AM2,△ACM为直角三角形,即72 (﹣2)2 (t 6)2=(﹣2 6)2 t2,解得t=﹣8,此时M点坐标为(﹣2,﹣8);当CM2 AM2=AC2,△ACM为直角三角形,即(﹣2 6)2 t 2)2 (t 6)2=72,解得t1=﹣3 
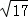,t2=﹣3﹣
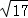,此时M点坐标为(﹣2,﹣3 
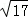)或(﹣2,﹣3﹣
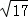).综上所述,M点的坐标为(﹣2,4)或(﹣2,﹣8)或(﹣2,﹣3 
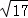)或(﹣2,﹣3﹣
).
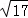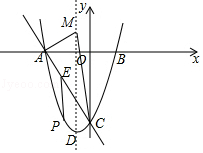[点评]本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和勾股定理的逆定理;会利用待定系数法求函数解析式;理解坐标与图形性质,记住两点间的距离公式;会利用分类讨论的思想解决数学问题.
