(1)见解析(2)0<p<0.3
(1)见解析(2)0
发布时间:2025-07-06 21:17:24
(1)见解析(2)0
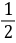 1.17×
1.17×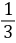 =1.18.由题设得X~B(2,p),即X的分布列为X012P(1-p)22p(1-p)p2所以X2的分布列为X21.31.250.2P(1-p)22p(1-p)p2∴E(X2)=1.3×(1-p)2 1.25×2p(1-p) 0.2×p2=1.3×(1-2p p2) 2.5×(p-p2) 0.2×p2=-p2-0.1p 1.3.(2)由E(X1)
=1.18.由题设得X~B(2,p),即X的分布列为X012P(1-p)22p(1-p)p2所以X2的分布列为X21.31.250.2P(1-p)22p(1-p)p2∴E(X2)=1.3×(1-p)2 1.25×2p(1-p) 0.2×p2=1.3×(1-2p p2) 2.5×(p-p2) 0.2×p2=-p2-0.1p 1.3.(2)由E(X1)