在△ABC中,∠C=90°,CD⊥AB于点D,E为AB的中点,AF⊥CE交CE的延长线于点F,连结DF,求证:四边形AFDC是等腰梯形.
在△ABC中,∠C=90°,CD⊥AB于点D,E为AB的中点,AF⊥CE交CE的延长线于点F,连结DF,求证:四边形AFDC是等腰梯形.
发布时间:2025-03-05 13:02:54
在△ABC中,∠C=90°,CD⊥AB于点D,E为AB的中点,AF⊥CE交CE的延长线于点F,连结DF,求证:四边形AFDC是等腰梯形.
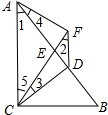 ∵CD⊥AB,AF⊥CE,∴∠AFC=∠ADC=90°,又∵AC为△AFC和△ADC的公共斜边,∴A、C、D、F四点共圆,∴∠1=∠2,∠3=∠4,∵∠C=90°,E为AB的中点,∴CE=
∵CD⊥AB,AF⊥CE,∴∠AFC=∠ADC=90°,又∵AC为△AFC和△ADC的公共斜边,∴A、C、D、F四点共圆,∴∠1=∠2,∠3=∠4,∵∠C=90°,E为AB的中点,∴CE=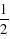 AB=AE,∴∠1=∠5,∴∠2=∠5,∴AC∥DF,又∵AC≠DF,∴四边形AFDC是梯形,∵∠1 ∠4=∠5 ∠3,即∠FAC=∠DCA,∴四边形AFDC是等腰梯形.
AB=AE,∴∠1=∠5,∴∠2=∠5,∴AC∥DF,又∵AC≠DF,∴四边形AFDC是梯形,∵∠1 ∠4=∠5 ∠3,即∠FAC=∠DCA,∴四边形AFDC是等腰梯形.
