如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.(1)求∠ADB的度数;(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;(3)在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.https://bgk-photo.cdn.bcebos.com/37d12f2eb9389b508c2d64339535e5dde6116e85.jpg
如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=B
C、(1)求∠ADB的度数;(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;(3)在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.https://bgk-photo.cdn.bcebos.com/37d12f2eb9389b508c2d64339535e5dde6116e85.jpg
发布时间：2025-03-07 21:36:04
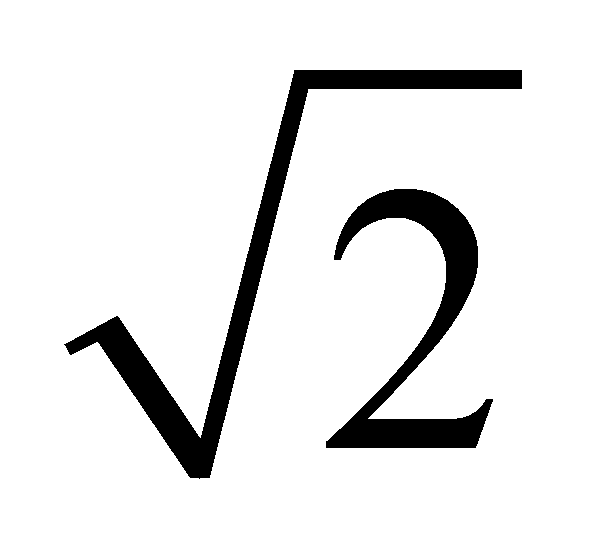[解析][分析](1)由直径所对的圆周角为直角及等腰三角形的性质和互余关系可得答案;(2)线段EA,CF,EF之间满足的等量关系为:EA2 CF2=EF2.如图2,设∠ABE=α,∠CBF=β,先证明α β=45°,再过B作BN⊥BE,使BN=BE,连接NC,判定△AEB≌△CNB(SAS)、△BFE≌△BFN(SAS),然后在Rt△NFC中,由勾股定理得:CF2 CN2=NF2,将相关线段代入即可得出结论;(3)如图3,延长GE,HF交于K,由(2)知EA2 CF2=EF2,变形推得S△ABC=S矩形BGKH,S△BGM=S四边形COMH,S△BMH=S四边形AGMO,结合已知条件S四边形AGMO:S四边形CHMO=8:9,设BG=9k,BH=8k,则CH=3 k,求得AE的长,用含k的式子表示出CF和EF,将它们代入EA2 CF2=EF2,解得k的值,则可求得答案.[详解]解:(1)如图1,
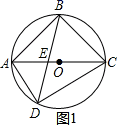∵AC为直径,∴∠ABC=90°,∴∠ACB ∠BAC=90°,∵AB=BC,∴∠ACB=∠BAC=45°,∴∠ADB=∠ACB=45°;(2)线段EA,CF,EF之间满足的等量关系为:EA2 CF2=EF2.理由如下:如图2,设∠ABE=α,∠CBF=β,
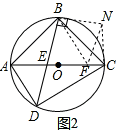∵AD∥BF,∴∠EBF=∠ADB=45°,又∠ABC=90°,∴α β=45°,过B作BN⊥BE,使BN=BE,连接NC,∵AB=CB,∠ABE=∠CBN,BE=BN,∴△AEB≌△CNB(SAS),∴AE=CN,∠BCN=∠BAE=45°,∴∠FCN=90°.∵∠FBN=α β=∠FBE,BE=BN,BF=BF,∴△BFE≌△BFN(SAS),∴EF=FN,∵在Rt△NFC中,CF2 CN2=NF2,∴EA2 CF2=EF2;(3)如图3,延长GE,HF交于K,
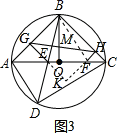由(2)知EA2 CF2=EF2,∴
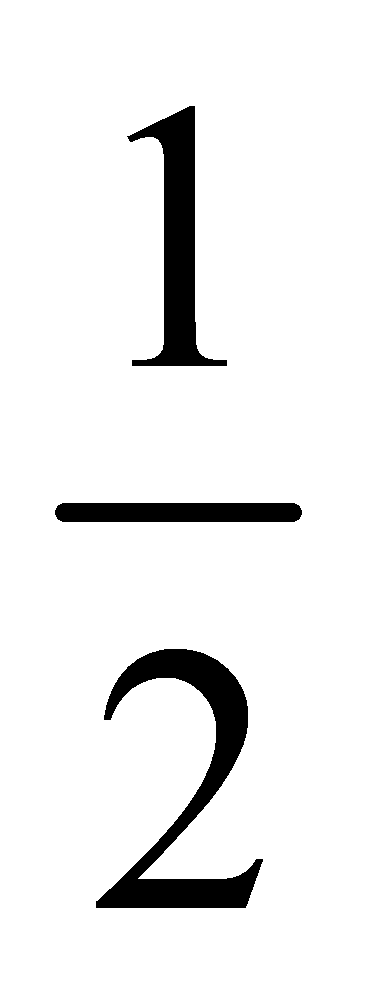EA2 
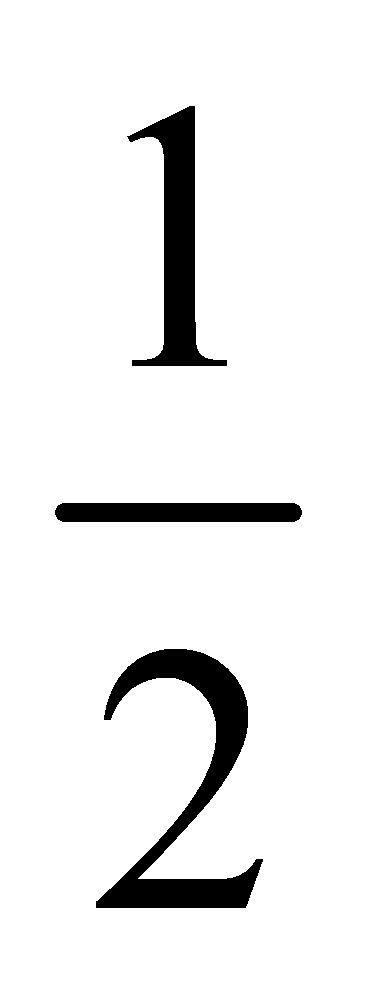CF2=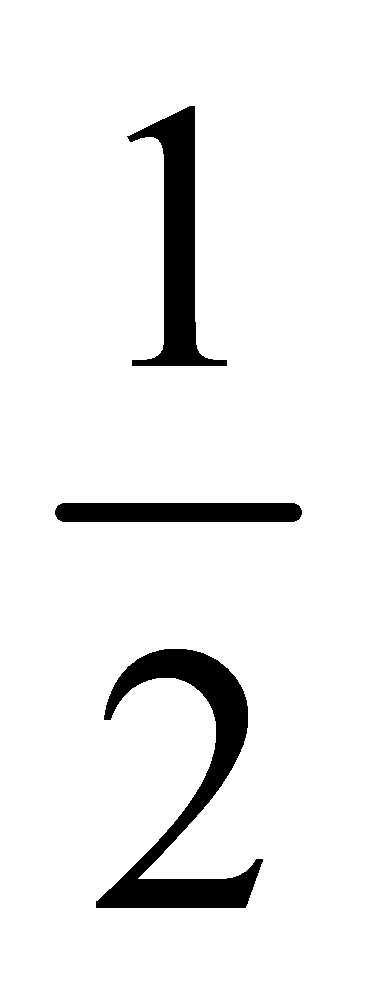
EF2,∴S△AGE S△CFH=S△EFK,∴S△AGE S△CFH S五边形BGEFH=S△EFK S五边形BGEFH,即S△ABC=S矩形BGKH,∴
S△ABC=
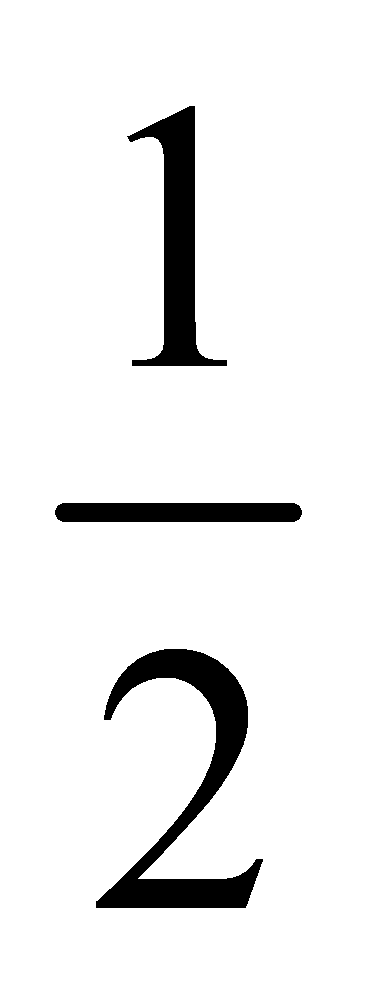S矩形BGKH,∴S△GBH=S△ABO=S△CBO,∴S△BGM=S四边形COMH,S△BMH=S四边形AGMO,∵S四边形AGMO:S四边形CHMO=8:9,∴S△BMH:S△BGM=8:9,∵BM平分∠GBH,∴BG:BH=9:8,设BG=9k,BH=8k,∴CH=3 k,∵AG=3,∴AE=3
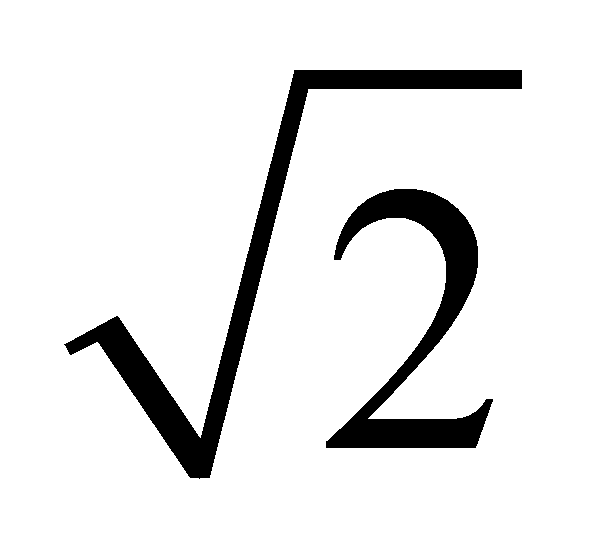,∴CF=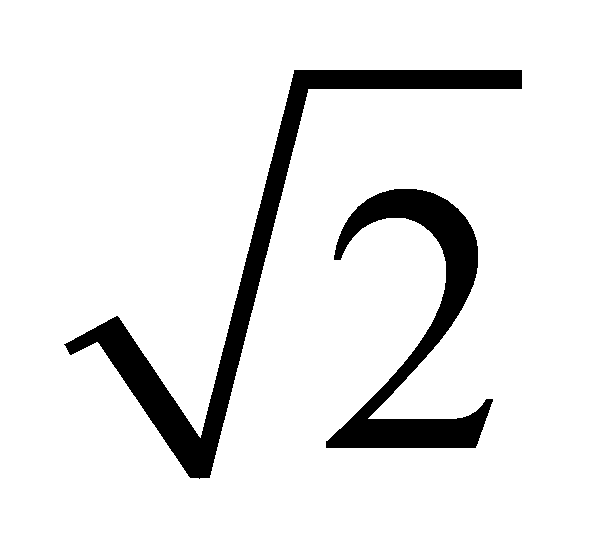
(k 3),EF=
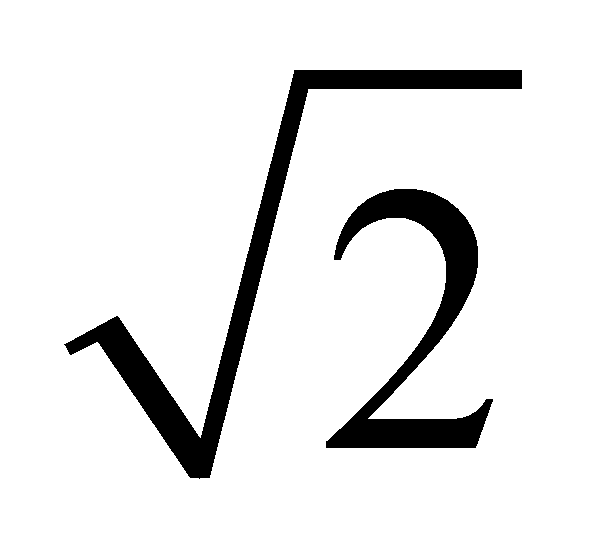(8k﹣3),∵EA2 CF2=EF2,∴
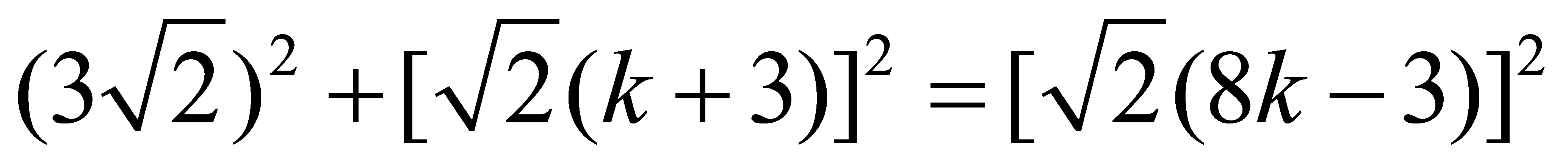,整理得:7k2﹣6k﹣1=0,解得:k1=﹣
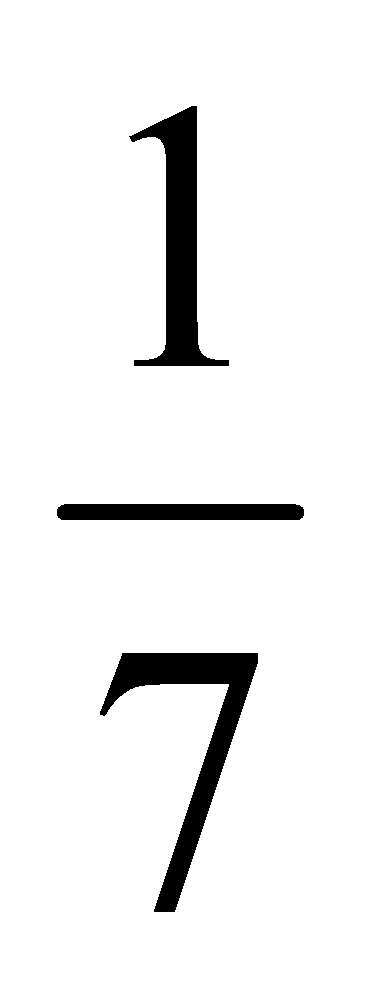(舍去),k2=1.∴AB=12,∴AO=
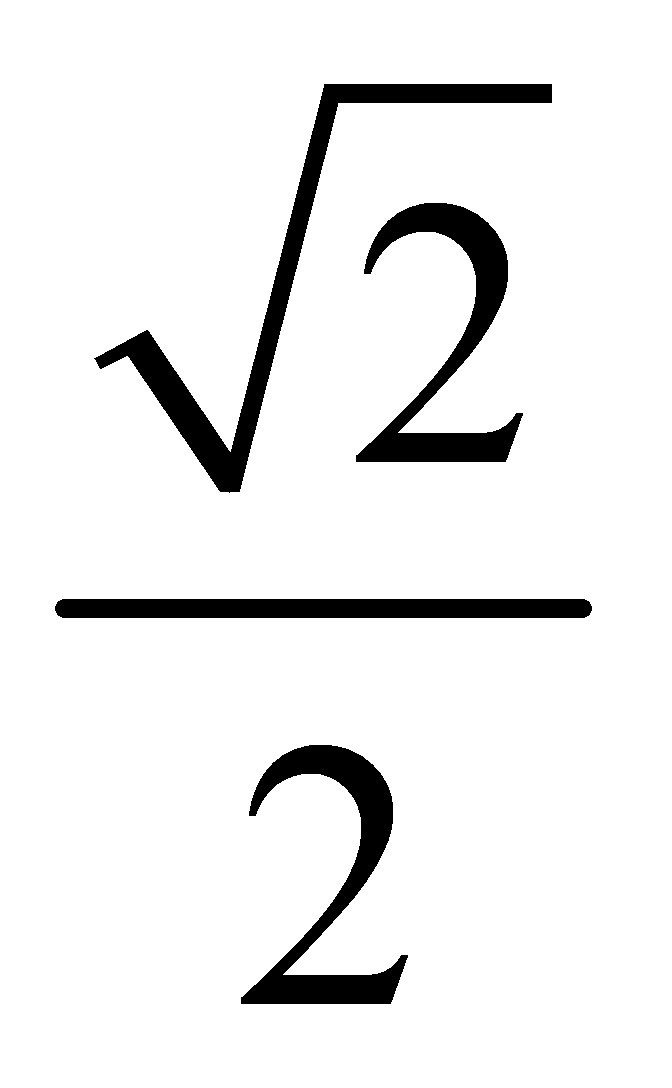AB=6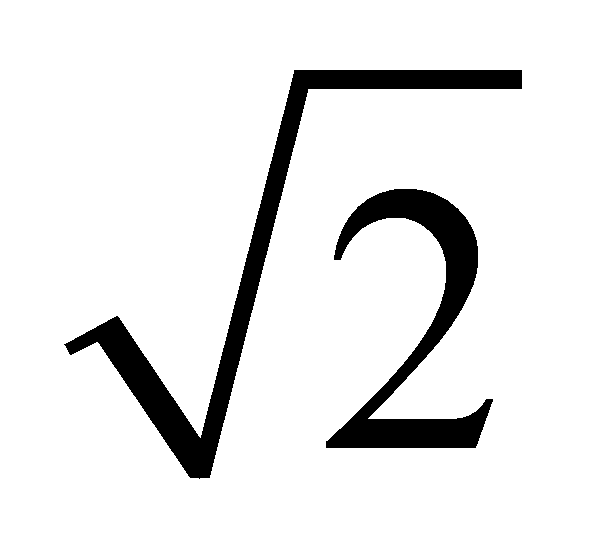
,∴⊙O的半径为6
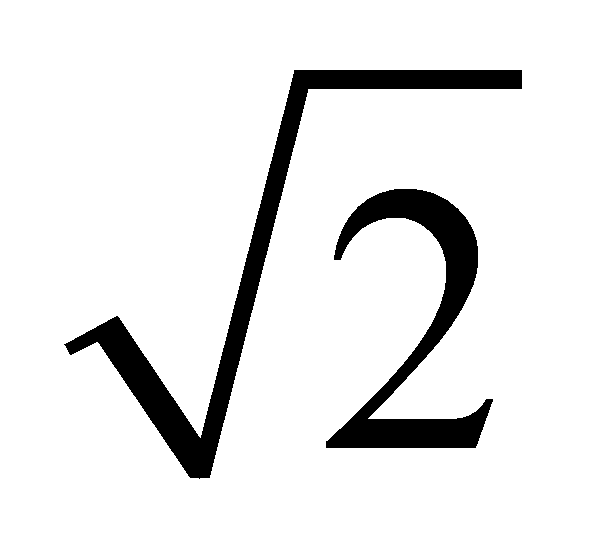.[点睛]本题属于圆的综合题,考查了圆的相关性质及定理、全等三角形的判定与性质、多边形的面积公式、勾股定理及解一元二次方程等知识点,熟练运用相关性质及定理是解题的关键.
