在曲线y=1-x2(x≥0,y≥0)上找一点(x0,y0),过此点作一切线与x轴、y轴围成一个三角形.(1)求三角形面积S的最小值及相应的x0;(2)当三角形面积达到最小值时,求此三角形的外接圆方程.
在曲线y=1-x2(x≥0,y≥0)上找一点(x0,y0),过此点作一切线与x轴、y轴围成一个三角形.(1)求三角形面积S的最小值及相应的x0;(2)当三角形面积达到最小值时,求此三角形的外接圆方程.
发布时间:2025-09-08 08:16:39
在曲线y=1-x2(x≥0,y≥0)上找一点(x0,y0),过此点作一切线与x轴、y轴围成一个三角形.(1)求三角形面积S的最小值及相应的x0;(2)当三角形面积达到最小值时,求此三角形的外接圆方程.
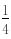 (
(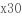 2x0
2x0 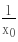 ),则S′=
),则S′=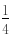 (3
(3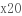 2-
2-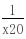 ),令S'=0得x0=
),令S'=0得x0=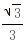 当x∈(0,
当x∈(0,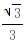 )时,S'<0,f(x0)单调递减; 当x∈(
)时,S'<0,f(x0)单调递减; 当x∈(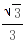 ,1)时,S'>0,f(x0)单调递增.∴S的最小值为
,1)时,S'>0,f(x0)单调递增.∴S的最小值为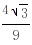 ,此时x0=
,此时x0=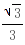 (7分)(2)当三角形面积最小时,切线方程为y=-
(7分)(2)当三角形面积最小时,切线方程为y=-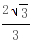 x
x 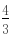 ,切线与x、y轴的交点分别为A(
,切线与x、y轴的交点分别为A(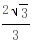 ,0)、B(0,
,0)、B(0,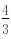 ),∴此三角形的外接圆圆心为(
),∴此三角形的外接圆圆心为(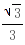 ,
,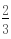 ),半径为
),半径为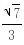 ,∴所求外接圆方程(x-
,∴所求外接圆方程(x-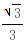 )2 (y-
)2 (y-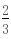 )2=
)2=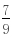 (12分)
(12分)
