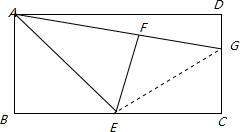
(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.(2)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.https://bgk-photo.cdn.bcebos.com/377adab44aed2e733b2ce34d9701a18b86d6fa8e.jpg解答:(1)猜想线段GF=GC,
(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.(2)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.https://bgk-photo.cdn.bcebos.com/377adab44aed2e733b2ce34d9701a18b86d6fa8e.jpg解答:(1)猜想线段GF=GC,
发布时间：2025-03-23 18:27:07
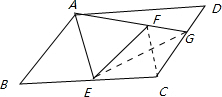∴BE=EF,∠B=∠AEF,∴EF=EC,∴∠EFC=∠ECF,∵矩形ABCD改为平行四边形,∴∠B=∠D,∵∠ECD=180°﹣∠D,∠EFG=180°﹣∠AEF=180°﹣∠B=180°﹣∠D,∴∠ECD=∠EFG,∴∠GFC=∠GFE﹣∠EFC=∠ECG﹣∠ECF=∠GCF,∴FG=CG;
