已知a为常数,函数f(x)=ex-2-ax.(1)讨论函数f(x)的单调性.(2)若函数f(x)有两个不同的零点x1,x2(x1<x2).①求实数a的取值范围;②证明:x1 x2>2.
已知a为常数,函数f(x)=ex-2-ax.(1)讨论函数f(x)的单调性.(2)若函数f(x)有两个不同的零点x1,x2(x1
发布时间:2025-05-22 17:52:28
已知a为常数,函数f(x)=ex-2-ax.(1)讨论函数f(x)的单调性.(2)若函数f(x)有两个不同的零点x1,x2(x1
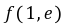 .所以实数a的取值范围为
.所以实数a的取值范围为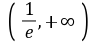 .②证明:由ex-2-ax=0,得x-2=ln(ax)=ln a ln x,即x-2-ln x=ln a.所以x1-2-ln x1=x2-2-ln x2=ln a.令g(x)=x-2-ln x,则g′(x)=1-
.②证明:由ex-2-ax=0,得x-2=ln(ax)=ln a ln x,即x-2-ln x=ln a.所以x1-2-ln x1=x2-2-ln x2=ln a.令g(x)=x-2-ln x,则g′(x)=1-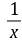 .当x>1时,g′(x)>0;当0
.当x>1时,g′(x)>0;当0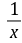
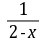 =
=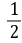 [x (2-x)]
[x (2-x)]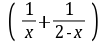 >2,所以h′(x)<0,即h(x)在(0,1)上单调递减.所以h(x)>h(1)=0,即g(x1)-g(2-x1)>0,所以x1 x2>2成立.
>2,所以h′(x)<0,即h(x)在(0,1)上单调递减.所以h(x)>h(1)=0,即g(x1)-g(2-x1)>0,所以x1 x2>2成立.