PA、PB、PC是从点P出发的三条射线,每两条射线的夹角为60°,求直线PC及平面PAB所成的角的余弦值.
P
A、P
B、PC是从点P出发的三条射线,每两条射线的夹角为60°,求直线PC及平面PAB所成的角的余弦值.
发布时间:2025-03-07 08:42:34
P
A、P
B、PC是从点P出发的三条射线,每两条射线的夹角为60°,求直线PC及平面PAB所成的角的余弦值.
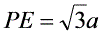 .在Rt△PDE中,∠DPE=60°,DE⊥PA,∴
.在Rt△PDE中,∠DPE=60°,DE⊥PA,∴ 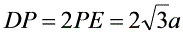 .在Rt△DPH中,DH⊥HP,PH=2a,
.在Rt△DPH中,DH⊥HP,PH=2a,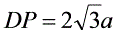 ,∴
,∴