已知函数f(x)=2x2 3(a2 a)lnx-8ax(Ⅰ)若x=3是f(x)的一个极值点求a的值;(Ⅱ)若函数f(x)在其导函数f(x)′的单调区间上也是单调的,求a的取值范围.
已知函数f(x)=2x2 3(a2 a)lnx-8ax(Ⅰ)若x=3是f(x)的一个极值点求a的值;(Ⅱ)若函数f(x)在其导函数f(x)′的单调区间上也是单调的,求a的取值范围.
发布时间:2025-08-08 16:48:16
已知函数f(x)=2x2 3(a2 a)lnx-8ax(Ⅰ)若x=3是f(x)的一个极值点求a的值;(Ⅱ)若函数f(x)在其导函数f(x)′的单调区间上也是单调的,求a的取值范围.
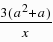 -8a=
-8a=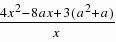 =
=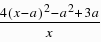 ,∵x=3是f(x)的一个极值,∴f′(3)=4(3-a)2-a2 3a=0,解得,a=4或a=3;而当a=3时,f′(x)≥0,故不成立,当a=4时,满足条件,故a=4.(II)f′(x)=4x
,∵x=3是f(x)的一个极值,∴f′(3)=4(3-a)2-a2 3a=0,解得,a=4或a=3;而当a=3时,f′(x)≥0,故不成立,当a=4时,满足条件,故a=4.(II)f′(x)=4x 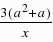 -8a=
-8a=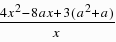 设g(x)=4x2-8ax 3(a2 a),△=16(a2-3a),设g(x)=0的两根为x1,x2,(x1<x2),(1)当△≤0,即0≤a≤3时,∴f(x)不单调,不满足题意;(2)当△>0,即a<0或a>3时,①若x1<0<x2,则
设g(x)=4x2-8ax 3(a2 a),△=16(a2-3a),设g(x)=0的两根为x1,x2,(x1<x2),(1)当△≤0,即0≤a≤3时,∴f(x)不单调,不满足题意;(2)当△>0,即a<0或a>3时,①若x1<0<x2,则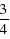 (a2 a)<0,即-1<a<0,此时,f(x)在(0,x2)上单调递减,在(x2, ∞)上单调递增,而f′(x)在(0, ∞)上单调递增,故不满足题意,②若x1<x2≤0,则
(a2 a)<0,即-1<a<0,此时,f(x)在(0,x2)上单调递减,在(x2, ∞)上单调递增,而f′(x)在(0, ∞)上单调递增,故不满足题意,②若x1<x2≤0,则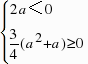 ,解得a≤-1,此时,f(x)在(0, ∞)上单调递增,满足题意;③若0<x1<x2,则
,解得a≤-1,此时,f(x)在(0, ∞)上单调递增,满足题意;③若0<x1<x2,则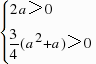 ,则a>0,此时,f(x)在(0,x1)上单调递增,在(x1,x2)上单调递减,在(x2, ∞)上单调递增,不满足题意;综上所述,a的取值范围为(-∞,-1].
,则a>0,此时,f(x)在(0,x1)上单调递增,在(x1,x2)上单调递减,在(x2, ∞)上单调递增,不满足题意;综上所述,a的取值范围为(-∞,-1].
