在平面直角坐标系中,抛物线y=(x﹣h)2 k的对称轴是直线x=1.若抛物线与x轴交于原点,求k的值;当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求k的取值范围.
在平面直角坐标系中,抛物线y=(x﹣h)2 k的对称轴是直线x=1.若抛物线与x轴交于原点,求k的值;当﹣1
发布时间:2025-04-02 14:36:14
在平面直角坐标系中,抛物线y=(x﹣h)2 k的对称轴是直线x=1.若抛物线与x轴交于原点,求k的值;当﹣1
 ①,点C的坐标为:(﹣4,8).设直线BC的解析式为:y=kx b,则
①,点C的坐标为:(﹣4,8).设直线BC的解析式为:y=kx b,则 解得:
解得: 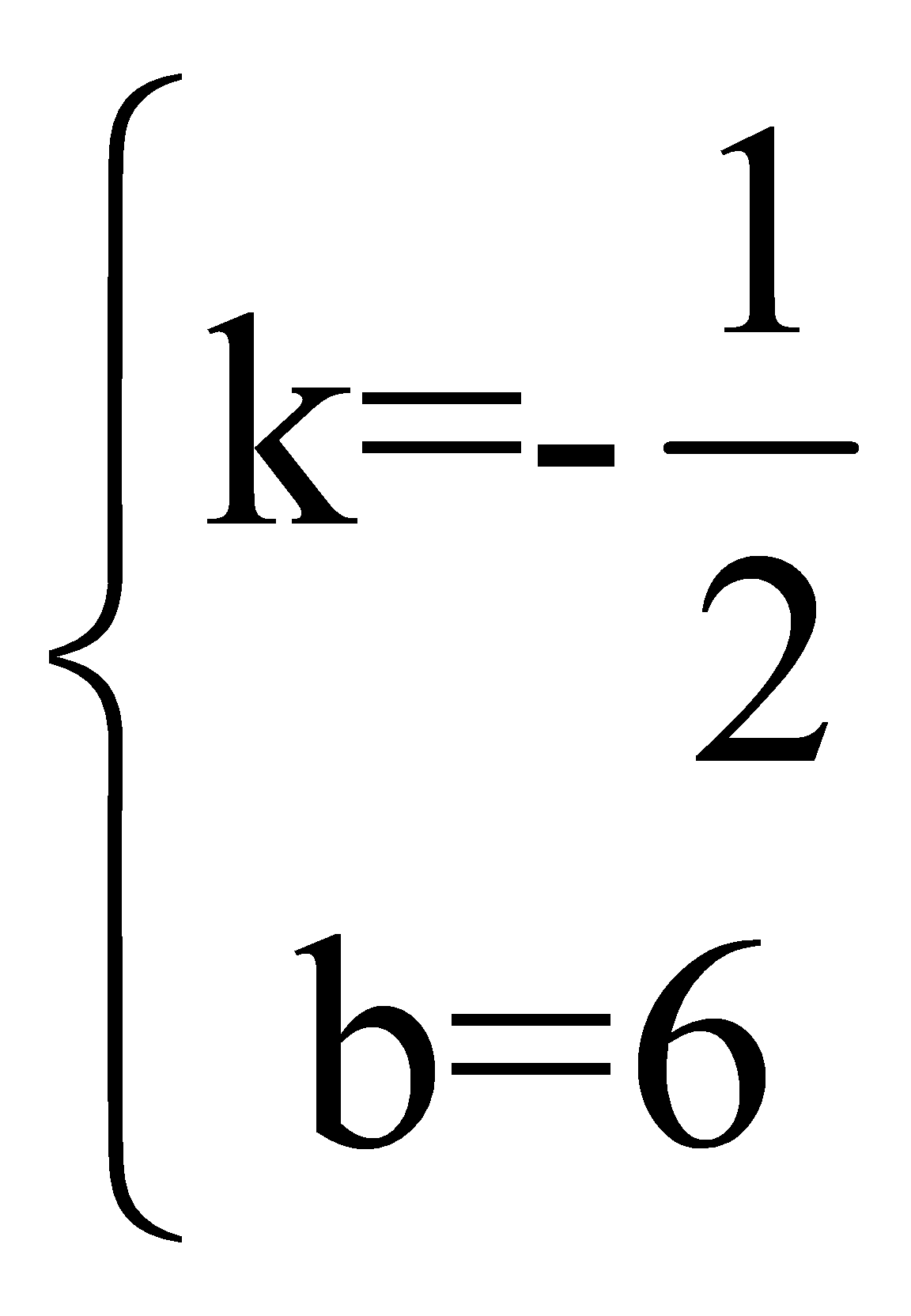 ∴直线BC的解析式为:y=﹣
∴直线BC的解析式为:y=﹣ x 6②,联立①②得:
x 6②,联立①②得:  或
或 (舍去),∴点E的坐标为:(﹣2,7).故答案为(﹣2,7).
(舍去),∴点E的坐标为:(﹣2,7).故答案为(﹣2,7).
