直线l与抛物线y2=2x相交于A、B两点,O为抛物线的顶点,若OA⊥OB.证明:直线l过定点.
直线l与抛物线y2=2x相交于
A、B两点,O为抛物线的顶点,若OA⊥O
B、证明:直线l过定点.
发布时间:2025-09-17 08:14:48
直线l与抛物线y2=2x相交于
A、B两点,O为抛物线的顶点,若OA⊥O
B、证明:直线l过定点.
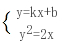 消去y得k2x2 (2kb-2)x b2=0由题意:x1x2=
消去y得k2x2 (2kb-2)x b2=0由题意:x1x2=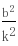
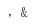 y1y2=(kx1 b)(kx2 b)=
y1y2=(kx1 b)(kx2 b)=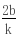 (5分)又由OA⊥OB得x1x2 y1y2=0,(7分)即
(5分)又由OA⊥OB得x1x2 y1y2=0,(7分)即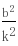
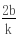 =0,解得b=0(舍去)或b=-2k(9分)故直线l的方程为:y=kx-2k=k(x-2),故直线过定点(2,0)(11分)(II)当直线l不存在斜率时,设它的方程为x=m,显然m>0联立方程得:
=0,解得b=0(舍去)或b=-2k(9分)故直线l的方程为:y=kx-2k=k(x-2),故直线过定点(2,0)(11分)(II)当直线l不存在斜率时,设它的方程为x=m,显然m>0联立方程得: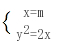 解得y=±
解得y=±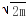 ,即y1y2=-2m又由OA⊥OB得x1x2 y1y2=0,即m2-2m=0,解得m=0(舍去)或m=2可知直线l方程为:x=2,故直线过定点(2,0)综合(1)(2)可知,满足条件的直线过定点(2,0).
,即y1y2=-2m又由OA⊥OB得x1x2 y1y2=0,即m2-2m=0,解得m=0(舍去)或m=2可知直线l方程为:x=2,故直线过定点(2,0)综合(1)(2)可知,满足条件的直线过定点(2,0).
