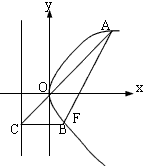
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴, 证明直线AC经过原点O。
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于
A、B两点,点C在抛物线的准线上,且BC∥x轴, 证明直线AC经过原点O。
发布时间:2025-03-21 17:16:12
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于
A、B两点,点C在抛物线的准线上,且BC∥x轴, 证明直线AC经过原点O。
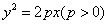 的焦点为
的焦点为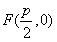 ,所以经过点F的直线AB的方程可设为
,所以经过点F的直线AB的方程可设为 ,代入抛物线方程得
,代入抛物线方程得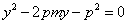 ,若记
,若记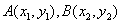 ,则
,则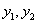 是该方程的两个根,所以
是该方程的两个根,所以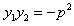 ,因为BC∥x轴,且点C在准线
,因为BC∥x轴,且点C在准线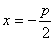 上,所以点C的坐标为
上,所以点C的坐标为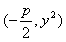 ,故直线CO的斜率为
,故直线CO的斜率为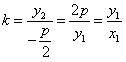 ,即k也是直线OA的斜率,所以直线AC经过原点O。
,即k也是直线OA的斜率,所以直线AC经过原点O。