设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.(1)若点P到直线x=-1的距离为d,A(-1,1),求 |PA| d的最小值;(2)若B(3,2),求 |PB| |PF|的最小值.
设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.(1)若点P到直线x=-1的距离为d,A(-1,1),求 |PA| d的最小值;(2)若B(3,2),求 |PB| |PF|的最小值.
发布时间:2025-08-14 20:36:37
设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.(1)若点P到直线x=-1的距离为d,A(-1,1),求 |PA| d的最小值;(2)若B(3,2),求 |PB| |PF|的最小值.
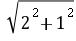 =
= .
.
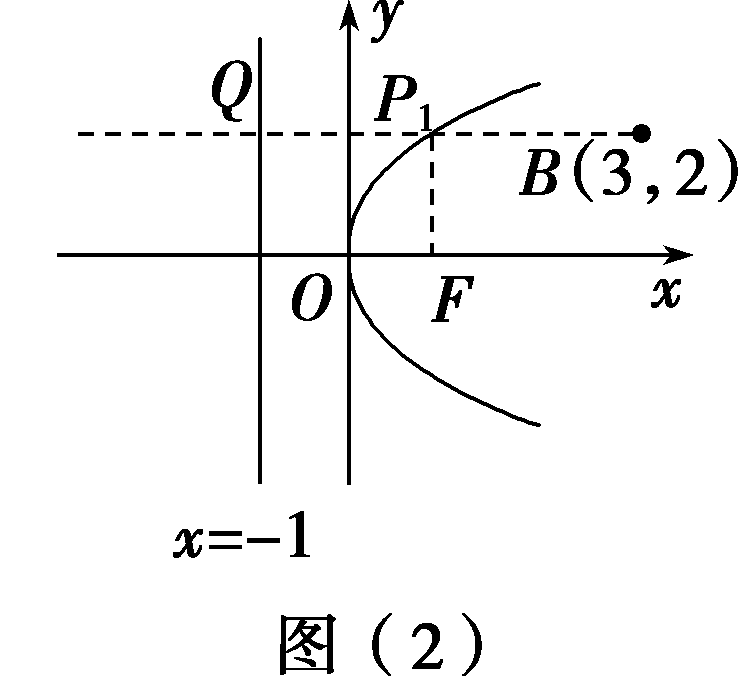 (2)把点B的横坐标代入y2=4x中,得y=±2
(2)把点B的横坐标代入y2=4x中,得y=±2 ,因为2
,因为2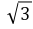 >2,所以点B在抛物线内部.自点B作BQ垂直准线于点Q,交抛物线于点P1(如图(2)所示).由抛物线的定义,知 |P1Q|=|P1F|,则 |PB| |PF|≥|P1B| |P1Q|=|BQ|=3 1=4.即 |PB| |PF|的最小值为4.[C 拓展探究]
>2,所以点B在抛物线内部.自点B作BQ垂直准线于点Q,交抛物线于点P1(如图(2)所示).由抛物线的定义,知 |P1Q|=|P1F|,则 |PB| |PF|≥|P1B| |P1Q|=|BQ|=3 1=4.即 |PB| |PF|的最小值为4.[C 拓展探究]
