（10分）在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．https://bgk-photo.cdn.bcebos.com/30adcbef76094b362126f692b3cc7cd98d109d1d.jpg（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB AN＝https://bgk-photo.cdn.bcebos.com/80cb39dbb6fd5266247ed16bbb18972bd407367c.jpgAM．
（10分）在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点
D、https://bgk-photo.cdn.bcebos.com/30adcbef76094b362126f692b3cc7cd98d109d1d.jpg（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB AN＝https://bgk-photo.cdn.bcebos.com/80cb39dbb6fd5266247ed16bbb18972bd407367c.jpgAM．
发布时间：2025-03-13 19:56:34
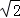，∵∠AMN＝30°，∴∠BMD＝180°﹣90°﹣30°＝60°，∴∠MBD＝30°，∴BM＝2DM，由勾股定理得，BM2﹣DM2＝BD2，即（2DM）2﹣DM2＝（
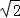）2，解得，DM＝
，∴AM＝AD﹣DM＝
﹣
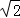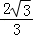；（2）证明：∵AD⊥BC，∠EDF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，
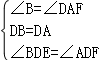，∴△BDE≌△ADF（ASA）∴BE＝AF；（3）证明：过点M作ME∥BC交AB的延长线于E，∴∠AME＝90°，则AE＝
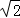AM，∠E＝45°，∴ME＝MA，∵∠AME＝90°，∠BMN＝90°，∴∠BME＝∠AMN，在△BME和△AMN中，
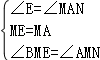，∴△BME≌△AMN（ASA），∴BE＝AN，∴AB AN＝AB BE＝AE＝
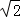AM．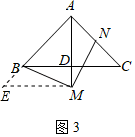
【点评】本题考查的是等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键．
